Absorption von Licht

Wir betrachten eine Schicht mit dem Brechungsindex n und der Dicke d, auf deren Oberfläche Licht parallel zur Oberflächennormalen einfällt.

Fällt elektromagnetische Strahlung auf Materie, so wird ein Teil der Strahlung reflektiert, der andere Teil dringt in das Medium ein. Dort wird die Strahlung durch zwei Prozesse geschwächt: Absorption (Umwandlung der Energie in eine andere Energieform, wie z.B. in Wärme) und Streuung (Richtungsänderung). Beides wird als Extinktion bezeichnet. Im folgenden soll nur die Absorption diskutiert werden. Nicht absorbierte Strahlung wird das Medium wieder verlassen. Dies ist insbesondere bei transparenten Medien der Fall, die wir bisher betrachtet haben. Die Energiebilanz im Falle monochromatischer Strahlung sieht folgendermaßen aus:

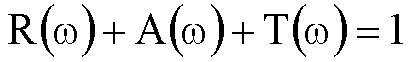
Hierin bezeichnen R den reflektierten Energieanteil, A die absorbierte Energie und T die Transmission der Probe. Die spektrale Reinabsorption entspricht dem relativen Anteil der durch das Medium absorbierten Energie. R erhält man vermittels des Reflexionskoeffizienten. Es gilt

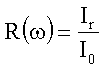
Für die spektrale Absorption A(w) erhält man dann zunächst

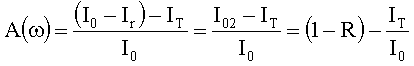
Statt dessen wird jedoch häufig der definierte Begriff der Reinabsorption verwendet, der sich auf die verbleibende Energie (Intensität) nach erfolgter Reflexion bezieht:

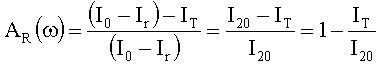
Für die Transmission ergibt sich aus der Gesamtenergiebilanz:

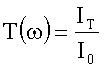
Die Durchlässigkeit der Probe ist jedoch definiert als

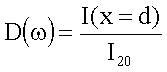
Wir untersuchen die Lichtabsorption eines Strahles der Anfangsintensität I₂₀ (nach der Reflexion) in der Schicht der Dicke d:

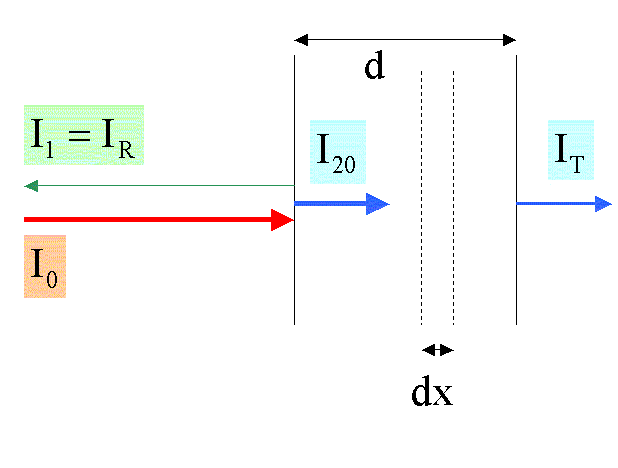
In einem Schichtelement der Dicke dx wird sich die Intensität um den Betrag

verringern. Den Proportionalitätsfaktor µ bezeichnet man als Absorptionskoeffizient des Materials. Die Integration der letzten Gleichung liefert nach Trennung der Variablen I und x das Lambert-Beer’sche Gesetz:

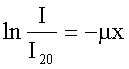
oder

Für die spektrale Reinabsorption gilt demzufolge

Für die Transmission erhalten wir mit I_r2 als reflektierter Intensität an der Probenrückseite (keine Mehrfachreflektionen):

bzw. bei gleichem Reflexionskoeffizienten an Vorder- und Rückseite der Schicht:

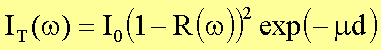
Die Durchlässigkeit beschreibt lediglich die Schwächung der Strahlung innerhalb der Schicht:

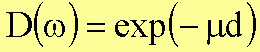
Durch die Messung von D kann man µ experimentell bestimmen. Da der Betrag von I₂₀ in der Regel schlecht zugänglich ist, kann µ auch durch Messung von I_T in Abhängigkeit von der durchstrahlten Schichtdicke d ermittelt werden. Trägt man ln I_T in Abhängigkeit von d auf, so ist aus dem Anstieg der Funktion ln I_T(d) direkt µ sowie aus dem Schnittpunkt mit der Ordinate I₀(1-R)² zu ermitteln.

Bei Dämpfung der Amplitude einer ebenen monochromatischen Welle durch Absorption ändert sich damit die Wellenfunktion zu

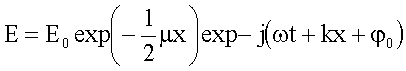
Der Faktor ½ in der Amplitude folgt aus der Proportionalität zwischen Intensität und Quadrat der Amplitude. Das Lambert’sche Gesetz gilt für die Dämpfung der Intensität.

Für nichtmagnetische, transparente Medien galt folgende Dispersionsbeziehung:

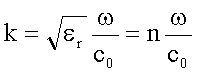
Damit schreibt sich die Wellenfunktion folgendermaßen:

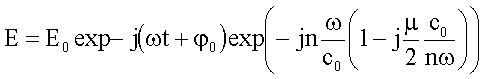
Mittels dieser Beziehung lässt sich der komplexe Brechungsindex n’ unter Verwendung von

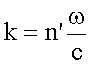
und

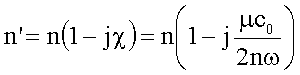
einführen. Der Imaginärteil nc des komplexen Brechungsindex bestimmt die Stärke der Absorption des Mediums und steht mit dem Absorptionskoeffizienten µ in folgendem Zusammenhang:

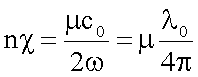
oder

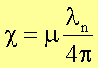
Hier ist die Vakuumwellenlänge mit l₀ und die Wellenlänge im Medium mit dem Brechungsindex n durch l_n bezeichnet. Im Gegensatz zu µ ([µ] = m^-1) ist c eine dimensionslose Größe. Mit n’ wird auch die dielektrische Permeabilität eine komplexe Größe. Es sei darauf hingewiesen, dass der Real- und Imaginärteil von e nicht unabhängig voneinander sind. Ist der Realteil von e im gesamten Frequenzbereich bekannt, so lässt sich daraus der Imaginärteil in Abhängigkeit von w berechnen. Dieser Zusammenhang besteht selbstverständlich auch umgekehrt. Die Zusammenhänge zwischen Real- und Imaginärteil der dielektrischen Permeabilität wurden von Kramers und Kronig abgeleitet, nach denen diese Relationen auch benannt sind.

Für absorbierende Medien (hier für n₁ = 1 und n₂ = n) erhält man den Reflexionskoeffizienten bei senkrechtem Einfall zu

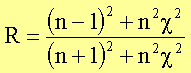
(Man erhält diese Relation aus der bereits bekannten Beziehung , indem man den reellen Brechungsindex durch den komplexen ersetzt und das Betragsquadrat von E_r/E_e berechnet.) Stark absorbierende Medien (c>>1) haben demnach einen hohen Reflexionskoeffizienten (metallische Reflexion). Einen hohen Absorptionsgrad (Anteil der absorbierten Energie), wie wir ihn bei schwarzen Körpern haben, setzt daher eine geringe Reflexion voraus. Die durch c bzw. m beschriebene Reinabsorption kann jedoch trotzdem hoch sein. Ist die Probe hinreichend dick, so ist A_R=1.

c >> 1	R ® 1	A ® 0	AR®1
niedriges c	R << 1	A ® 1	AR£1

Für Metalle besteht ein Zusammenhang zwischen Absorptionskoeffizient und Leitfähigkeit des Materials:

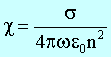
Damit gilt für R:

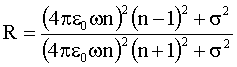
Für hinreichend hohe Leitfähigkeit haben wir metallische Reflexion (R=1) vorzuliegen. Der absorbierte Energieanteil ist sehr gering (A»0), wird jedoch in einer dünnen Oberflächenschicht umgesetzt (Skineffekt A_R»1)

In Lösungen schwächen i.a. nur die gelösten Moleküle das Licht. Hier ist µ der Konzentration der Moleküle c proportional und es gilt das Beersche Gesetz:

Die Größe a wird als molarer Extinktionskoeffizient bezeichnet. Wichtig ist dieser Zusammenhang für Konzentrationsbestimmungen mit Photometern. Ersetzt man c durch die Volumendichte der absorbierenden Teilchen N, so gilt

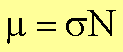
Die Größe s hat die Dimension eines Querschnittes und heißt Absorptionsquerschnitt. Während die effektive durch µ beschriebene Absorption von der Zahl und Dichte der absorbierenden Teilchen abhängt, ist s charakteristisch für die Wechselwirkung des einzelnen Teilchens mit der elektromagnetischen Strahlung.

Im allgemeinen ist die eingestrahlte Energie nicht spektral rein, wie etwa im Falle von Laserstrahlung. Weiterhin kann auch die Einfallsrichtung und Polarisation der Strahlung verschieden sein. Die Energiebilanzgleichung muss natürlich auch nach der Summation über alle spektralen Anteile gelten:

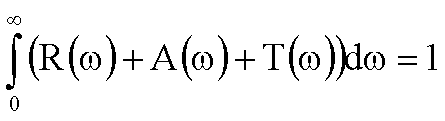
Die summierten Anteile lassen sich in der vereinfachten Gleichung

Hierin bezeichnen R den Reflexionsgrad (Reflexionsvermögen), A den Absorptionsgrad (Absorptionsvermögen) und T den Transmissionsgrad. Der Absorptionsgrad entspricht dem Anteil der insgesamt durch das Medium absorbierten Energie.