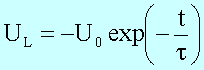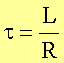Ein- und Ausschaltvorgang an einer Induktivität
![]()
![]()
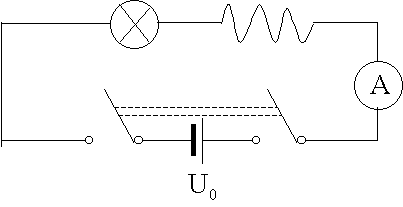
![]()
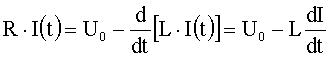
Differenzieren
nach t ergibt folgende Differentialgleichung:
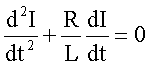
Mit
dem Lösungsansatz
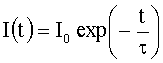
für
diese homogene Gleichung findet man für die Zeitkonstante t
Als spezielle Lösung der inhomogenen Gleichung
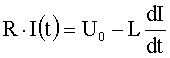
erhält
man
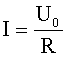
Die allgemeine Lösung erhält man als Summe aus der Lösung der homogenen und inhomogenen Gleichung:
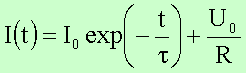
Einschaltvorgang
Anfangsbedingung: ![]()
Mit der oberen Bedingung erhält man ![]() und
und
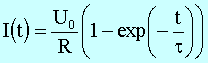
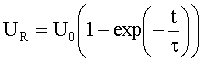
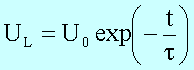
Beispiel:
Eine Spule mit N = 100 Windungen, d = 1cm und lS = 10 cm enthält einen Eisenkern mit µr = 1000. Diese Spule mit einem Widerstand von 1W werde mit einer Spannungsquelle von 5V verbunden..
Wir berechnen zunächst die Induktivität L mittels
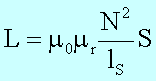
zu L = 9,9 mH. Die Zeitkonstante ergibt sich damit mittels
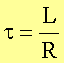
zu t = 9,9 ms.
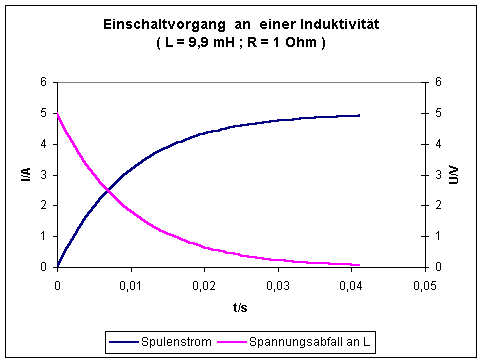
Ausschaltvorgang
Anfangsbedingung: 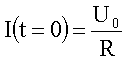
Mit Hilfe der homogenen Lösung (Spannung U0 abgeschaltet)
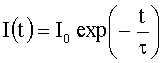
ergibt sich:
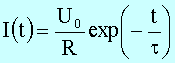
Die Spannung an L verhält sich folgendermaßen: