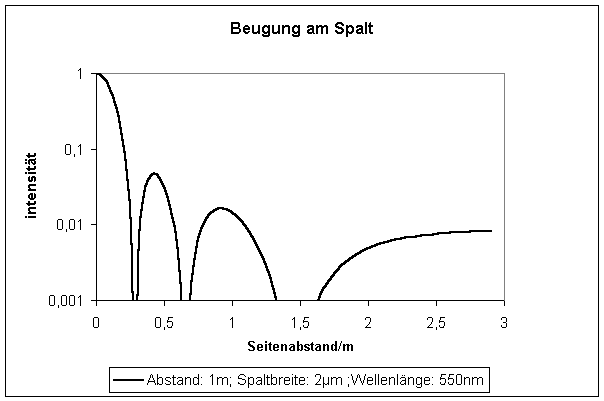
Fraunhofersche Beugung am Spalt

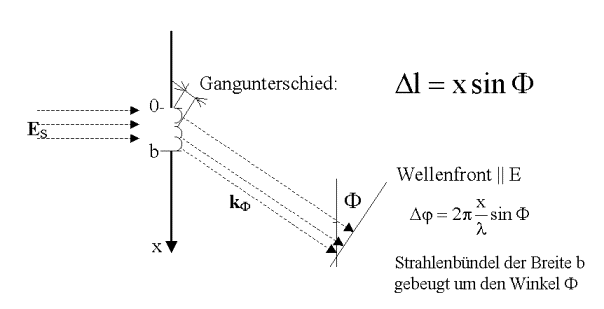
Phasendifferenz: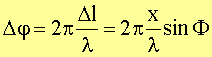

Jeder Punkt x der Öffnung ist Ausgangspunkt einer Elementarwelle (Huygenssches Prinzip). Die Superposition aller unter dem Winkel F gebeugten Teilstrahlen entspricht einer Summation der Feldstärken der von x = 0 bis x = b (bei festem F) in Richtung k_F ausgehenden Teilwellen und ergibt an der Wellenfront unter Beachtung der Phasenverhältnisse die Feldstärke

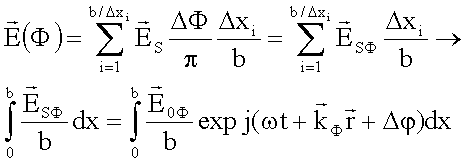
Das Winkelelement DF/p entspricht dem Anteil der vom Spalt b ausgehenden Elementarwellen, der in die Richtung F, F+DF gestreut wird. Das Verhältnis (Dx/b) entspricht einem Anteil des den Spalt b passierenden Strahlenbündels der Breite Dx.

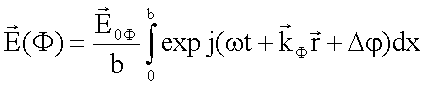
Unter Verwendung des Ausdruckes für die ortsabhängige Phasendifferenz 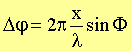erhalten wir die Feldstärke

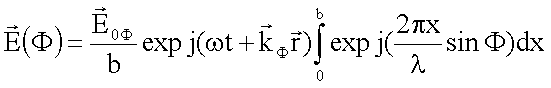
Damit erhält man die Amplitude der Feldstärke in Abhängigkeit vom Winkel F:

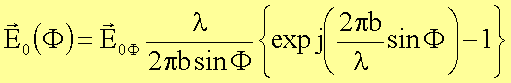
Die Intensität ist dem Quadrat des Betrages der Feldstärke proportional:

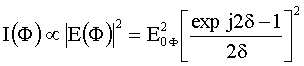
Mittels der Beziehungen

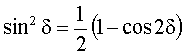
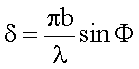
erhalten wir

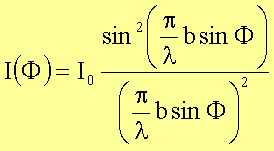
Intensitätsverteilung bei Beugung am Spalt

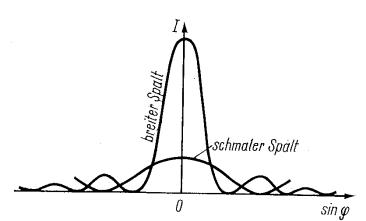
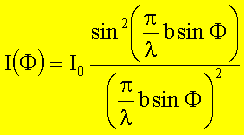
Berechnung der Intensitätsminima

Mit

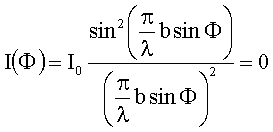
folgt

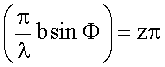
Daraus ergibt sich die Bedingung für Intensitätsminima zu

(Hinweis: Für die Beugung am Gitter ist dies die Bedingung für Intensitätsmaxima!)

Berechnung der Intensitätsmaxima

Es ist das Problem

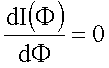
für das Auftreten relativer Maxima zu lösen.

Die Intensitätsgleichung lässt sich in der vereinfachten Form

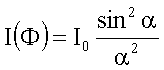
aufschreiben. Durch Differenzieren nach a und Nullsetzen folgt

Damit muss die transzendente Gleichung

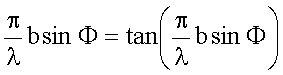
gelöst werden.

Diese Gleichung hat die Lösungen

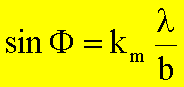
Wobei die Koeffizienten k_m Lösungen der Gleichung

sind mit