Die Reflexion von Licht

Die Fresnel’schen Formeln

Gegenstand dieses Kapitels ist die Berechnung der Intensität eines reflektierten Lichtstrahles, der aus einem Medium mit der Brechzahl n₁ kommend auf eine Grenzfläche mit der Brechzahl n₂ auftrifft.

Für die Intensität einer ebenen Welle gilt:

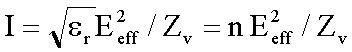
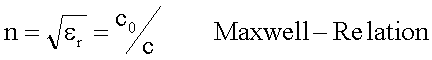
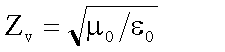
Als Einfallsebene des Lichtstrahles wählen wir die x-z-Ebene.

An der Grenzfläche gelten folgende Randbedingungen:

· Stetigkeit der Normalkomponente von D:

Diese Bedingung führt (wie die Stetigkeit der Parallelkomponente von k) zum Brechungsgesetz:

· Stetigkeit der Tangentialkomponente von E:

· Erhaltung der Normalkomponente des Energiestromes:

Einfallsebene sei die x-z-Ebene

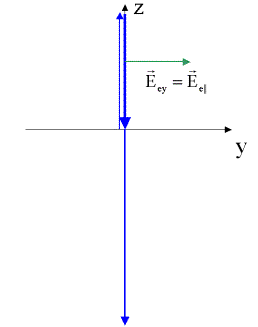
s-Welle

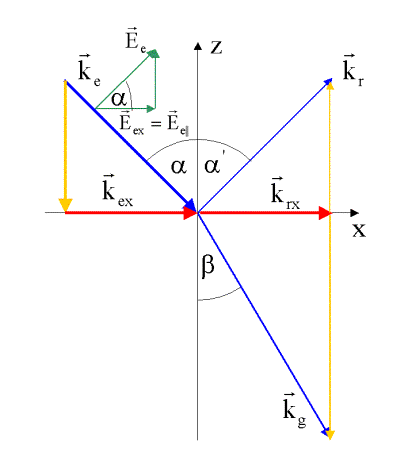
p-Welle

Polarisation des Lichtes senkrecht zur Einfallsebene (s-Wellen)

Mit und

erhält man die folgende Gleichung:

Die Intensitätsbedingung für die Normalkomponente des Poyntingvektors

schreibt sich folgendermaßen:

Eliminiert man aus beiden Gleichungen die Größe E_gy und verwendet das Brechungsgesetz, so erhält man folgende Beziehung zwischen den Effektivwerten der einfallenden (E_ey) und reflektierten (E_ry) Amplitude:

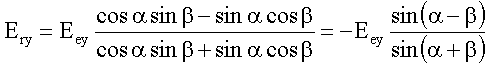
Für den Reflexionskoeffizienten gilt dann:

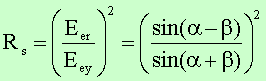
Im Spezialfall fast senkrechten Einfalls (cosa » 1, cosb »1) erhält man:

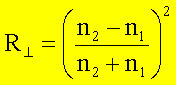
Polarisation des Lichtes in der Einfallsebene (p-Wellen)

Wegen der Stetigkeit der E-Komponenten in x-Richtung gilt

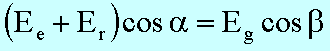
Die Bedingung für den Energiestrom ist analog:

Diesmal erhält man für den Reflexionskoeffizienten:

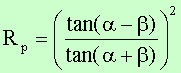
Für senkrechten Einfall gilt analog wie bei s-Wellen:

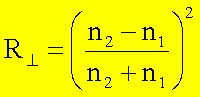
Für nahezu parallelen Einfall gilt für s-wie p-Wellen:

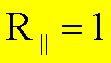
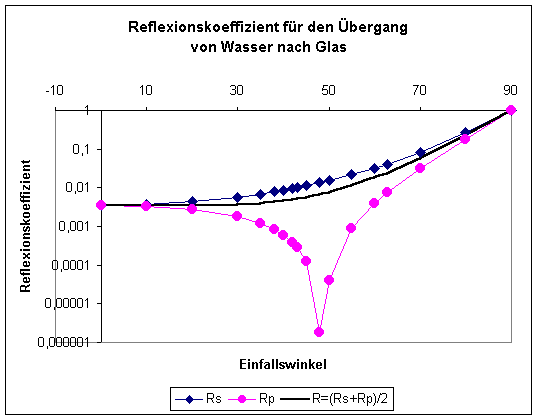
Im Falle a + b = 90° ist für p-Wellen R_p = 0. Man erhält dann mittels des Brechungsgesetzes das Brewster’sche Gesetz:

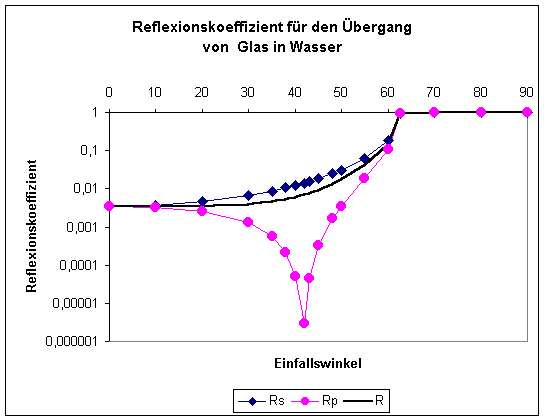
Rechenbeispiele für den Übergang Wasser-Glas und Glas-Wasser