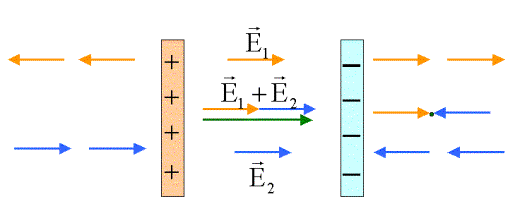
Feld und Kapazität eines Plattenkondensators

Im Außenraum des Plattenkondensators kompensieren sich die Felder der Ladungsverteilungen der beiden Einzelplatten.

Im Innenraum addieren sich die Felder der beiden Einzelplatten zu

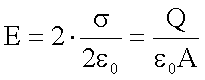
Daraus ergibt sich zwischen den Platten eine Potentialdifferenz zu

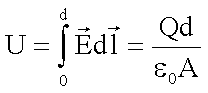
1Die Kapazität eines Kondensators gibt die gespeicherte Ladung bezogen auf die Potentialdifferenz an:

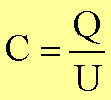
Daraus folgt für die Kapazität eines Plattenkondensators

,

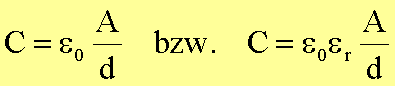falls das Feld E durch ein Dielektrikum abgeschirmt wird.

Plattenkondensator mit Dielektrikum

Zwischen den Platten eines Kondensators gilt:

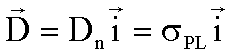
Das elektrische Feld ist durch das Dielektrikum zwischen den Kondensatorplatten abgeschirmt:

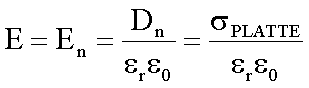
Andererseits ist das Feld E durch die Potentialdifferenz U zwischen den Platten und die Flächenladungsdichte s durch die Oberflächenladung Q bestimmt:

Damit erhält man für die Potentialdifferenz zwischen den Platten:

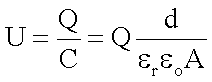
Misst man die Potentialdifferenz zwischen den Platten eines mit einer definierten Ladung aufgeladenen Kondensators (Q = const. ; Ladespannung abgetrennt), so gilt:

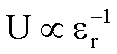
Hält man dagegen die Potentialdifferenz konstant, so ist die gespeicherte Ladung proportional zu e_r.

Energiespeicherung im Plattenkondensators

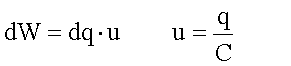
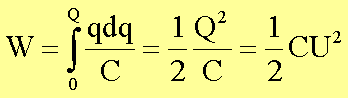
(Wegen C µ e_r gilt W µ e_r bei U = const. und W µ e_r^-1 bei Q = const)

Mit

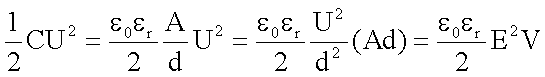
erhält man (mit dem Volumen V=Ad) für die Energiedichte :

(unabhängig von der Geometrie des Kondensators)

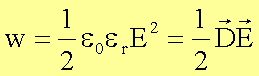
Die Energie eines geladenen Kondensators steckt im elektrischen Feld.