Wechselstromlehre
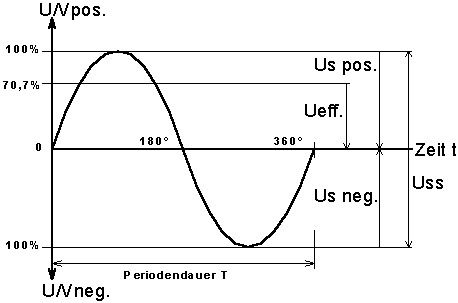
Wechselspannungen
sind zeitlich periodische Spannungen der Amplitude U0 (U0 =
Uss/2), der Grundfrequenz f
(f = 1/T) und der Phasenlage j.
Für die obere grafische Darstellung gilt:
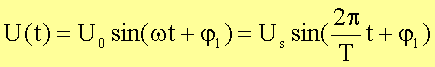
Im
Falle sinusförmiger Spannungen sind die in Stromkreisen fließenden Ströme
ebenfalls sinusförmig, jedoch im allgemeinen mit einer anderen Phasenlage j2:
Ohm’sche Widerstände im Wechselstromkreis
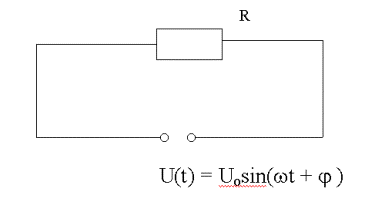
Die
Gesetze des Gleichstromkreises gelten im Wechselstromkreis für die
Momentanwerte, d.h. insbesondere:
|
U(t) = R.I(t) |
Ohm’sches Gesetz |
|
P(t) = U(t).I(t) |
Leistung |
Da die direkte Proportionalität zwischen Strom und Spannung am Ohm’schen Widerstand erhalten bleibt, besteht zwischen beiden Größen keine Phasenverschiebung, d.h. es gilt j1 = j2 = j.
Für
die Leistung führt man einen Mittelwert über die Periodendauer T ein:
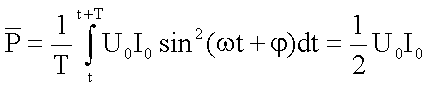
Damit
kann man wegen P = U.I = R.I2 = U2/R
auch schreiben:
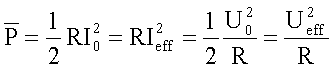
mit den Effektivwerten für Spannung und Strom
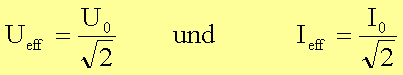
Eine
Gleichspannung mit dem Effektivwert Ueff setzt am Ohm’schen
Widerstand R dieselbe Leistung um, wie eine Wechselspannung mit der Amplitude U0.
Der Begriff des Effektivwertes kann auf beliebige zeitlich periodische
Spannungen ausgedehnt werden.
Beispiel Sägezahnspannung
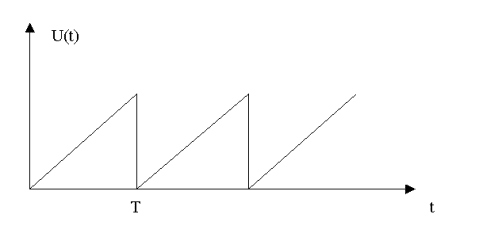
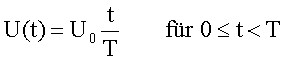
Für den zeitlichen Mittelwert erhält man:
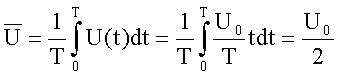
Für den Effektivwert (quadratischen Mittelwert) gilt:
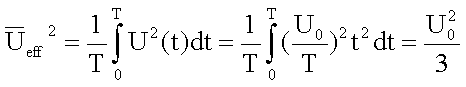
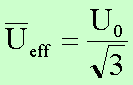
Dieses Ergebnis erhält man auch, wenn man die Sägezahnspannung als eine Überlagerung von Sinusspannungen darstellt und dann den Effektivwert für sinusförmige Spannungen verwendet. Eine periodische Spannung kann mittels Fourieranalyse in ein diskretes Frequenzspektrum zerlegt werden. Auf die einzelnen Spannungskomponenten können dann die Regeln für sinusförmige Spannungen angewandt werden.
Beispiel Sägezahnspannung
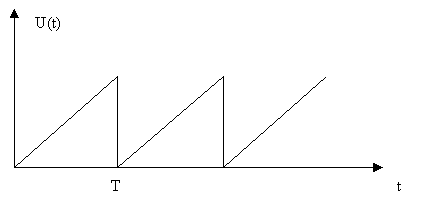
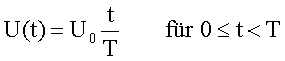
Die Entwicklung einer periodischen „Sägezahnspannung“ in eine Fourierreihe ergibt folgendes Frequenzspektrum:
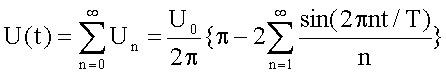
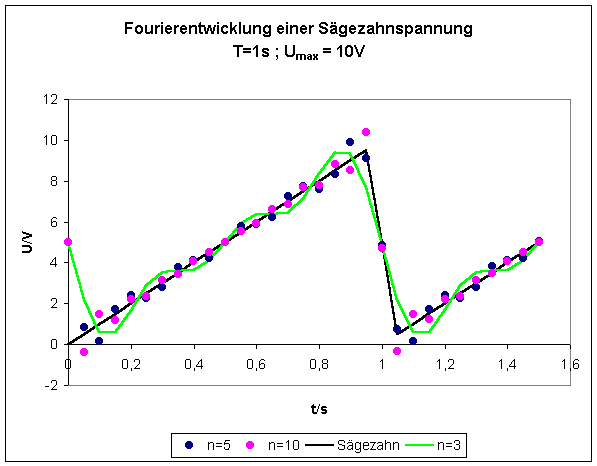
Zur Berechnung des Effektivwertes der Spannung summiert man die Effektivwerte (Leistungen) aller Summanden der Reihe:
Für
die Komponente n = 0 (Gleichspannungskomponente ) folgt:
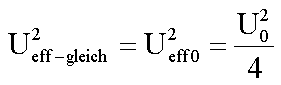
Für die sinusförmigen Komponenten erhält man:
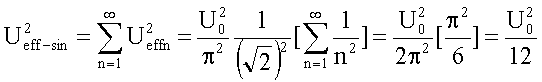
Die
Summe beider Beträge ergibt U2eff = U20/3
bzw. Ueff = U0/Ö3.
Dieses
Resultat stimmt mit vorheriger Rechnung überein.