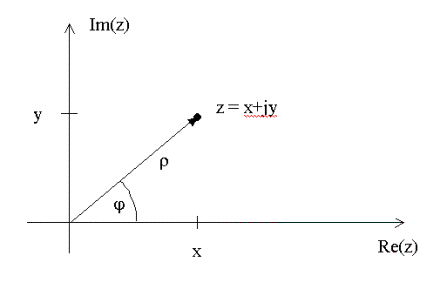
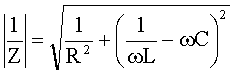Zeigerdiagramm und trigonometrische Darstellung einer komplexen Zahl

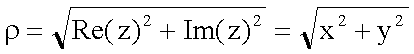
Exponentialdarstellung:

Die aus der Gleichstromlehre bekannten Gesetzmäßigkeiten für die Addition von Strömen und Spannungen, etwa die Kirchhoff’schen Gesetze, gelten in der Wechselstromlehre für die Momentanwerte. Will man die Effektiv- bzw. Maximalwerte von Spannung und Strom in der Rechnung verwenden, muss man die Phasenbeziehungen dieser Größen zueinander berücksichtigen. Die grafische Auftragung der Spannungen U(t) bzw. Ströme I(t) als Zeiger in einem Polardiagramm entspricht ihrer mathematischen Behandlung als komplexe Zahl. Die Zeigerlänge entspricht dem Betrag (der Amplitude) einer harmonischen Größe, der Winkel des Zeigers mit der reellen Achse dem Phasenwinkel j = wt+j₀. Die Projektion des Zeigers auf die reelle Achse ( u(t) = Re[U(t)] oder i(t) = Re[I(t)] ) entspricht dem Momentanwert der Spannung bzw. des Stromes. Wir betrachten zunächst die

Reihenschaltung von Wechselstromwiderständen

Es gilt der Maschensatz für die Momentanwerte

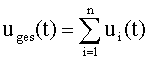
Trägt man die Spannungen in der Polarebene auf, so gilt folgende Zuordnung zwischen den Koordinaten und elektrischen Größen :

Der Strom ist bei einer Reihenschaltung überall gleich groß. Man misst die relative Phasenlage aller Spannungen bezüglich des Stromes. Da die Phasendifferenz zwischen Spannung und Strom am Ohm’schen Widerstand gleich Null ist, entspricht auch die Phasenlage der am Ohm’schen Widerstand abfallenden Spannung dem Wert j_0W = 0.

Betrachtet man die Verhältnisse zu einem beliebigen aber festen Zeitpunkt t = 0, so entsprechen die Phasenverschiebungen der einzelnen Spannungen u_i den Phasendifferenzen zum Spannungsabfall am gesamten Ohm’schen Widerstand, wenn wir per definitionem j_0W = 0 setzen. Tragen wir auf der reellen Achse den maximalen Spannungsabfall am Ohm’schen Widerstand auf, so erhalten wir eine Phasendifferenz von ± 90° zu dem Moment, wo an einer Induktivität resp. Kapazität ein maximaler Spannungsabfall vorliegt.

Aus der grafischen Addition aller Einzelspannungen erhält man die Gesamtspannung entsprechend dem Maschensatz. Der Winkel, den der Zeiger U_ges mit der reellen Achse einschließt, entspricht der Phasenverschiebung zwischen Spannung und Strom.

Die grafischen Verhältnisse sind in folgender Skizze dargelegt:

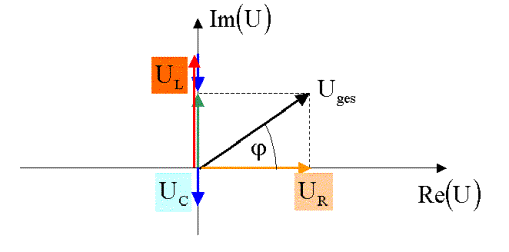
Für die Beträge der Spannungen (gemessen z.B. mit einem auf Effektivwert geeichten Voltmeter – u_eff = u₀/Ö2) erhält man mit

folgenden Zusammenhang:

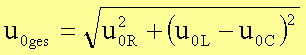
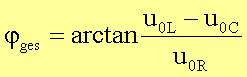
Für die Momentanwerte der Spannungen (gemessen z.B. mit einem Oszillographen) gilt dann mit der Schreibweise

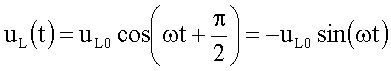
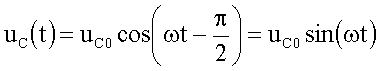
Wir betrachten im folgenden ein Beispiel – die Reihenschaltung aus einer Induktivität und einem Ohm’schen Widerstand. Es wird Netzspannung von u_eff = 220V angelegt. Am Widerstand R werde eine Spannung von u_effR = 180V gemessen. In der folgenden Tabelle sind die Amplituden, Effektivwerte und Phasenverschiebungen der einzelnen Spannungen gegenüber dem Strom aufgetragen:

	umax /V	ueff / V	j
uR	254,5	180	0°
uL	179	126,5	90°
uges	311	220	35,1°

Für diese Werte wurde folgendes Polardiagramm für zwei verschiedene Zeitpunkte berechnet:

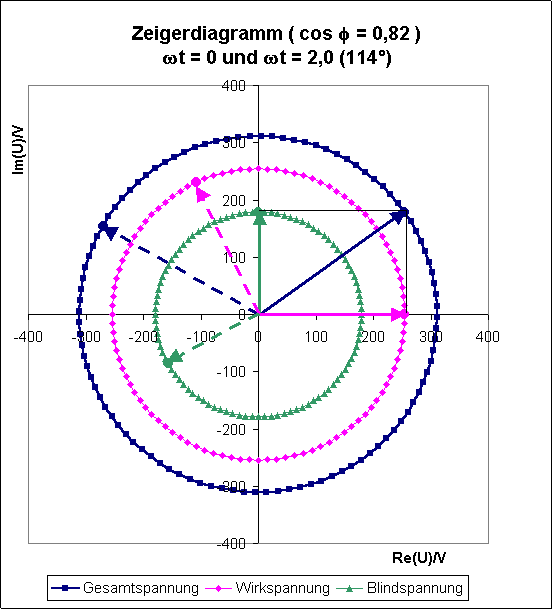
Aus der letzten Tabelle geht hervor, dass die Maximal- resp. Effektivwerte der Spannungen pythagoräisch addiert werden müssen. Dies gilt jedoch nicht für die Momentanwerte. Aus der folgenden Grafik geht hervor, dass die Summe der momentanen Spannungsabfälle an Induktivität und Ohm’schem Widerstand immer gleich dem Betrag des Momentanwertes der Gesamtspannung ist:

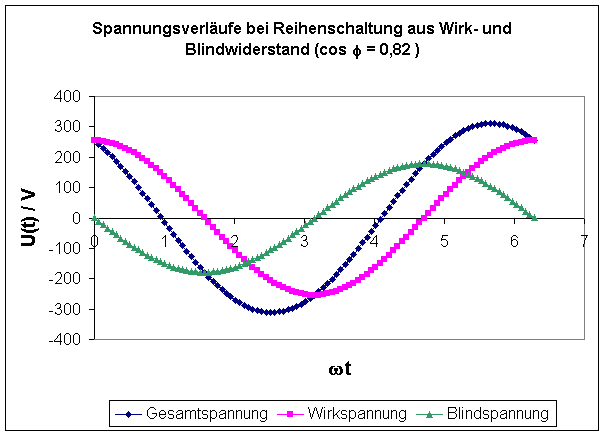
Der Spannungsabfall an R, C oder L kann einem Widerstand R resp. einer Impedanz X_C,L zugeordnet werden. Es gilt bei Reihenschaltung:

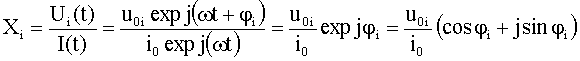
Wegen der Phasenverschiebung von ±90° an C oder L ist jedoch bei maximalem Strom der Spannungsabfall gleich Null (cos j_L,C = 0, sinj_L,C = ±1). Aus diesem Grunde sind die Impedanzen von C und L imaginäre Größen.

Wir hatten bereits gefunden:

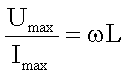und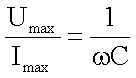

Somit gilt:

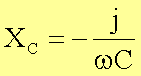
Diese Widerstände können analog zur Spannung in einem Zeigerdiagramm dargestellt und pythagoräisch addiert werden:

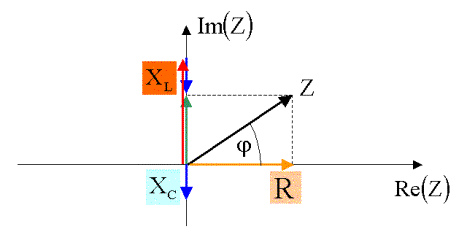
Für den Gesamtwiderstand Z einer Reihenschaltung aus R,C und L gilt somit:

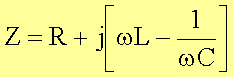
Für den Betrag von Z gilt dann:

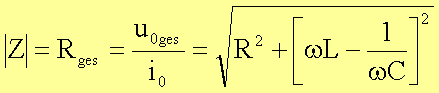
Der Widerstand hat ein Extremum (Minimum) vom Betrag R_ges = R im Fall:

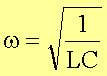
Letztere Relation heißt auch Thomson’sche Schwingkreisformel.

Parallelschaltung von Wechselstromwiderständen

Bei der Parallelschaltung von Widerständen gilt der Knotensatz, in diesem Fall für die Momentanwerte der Ströme:

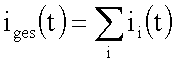
Trägt man die Ströme in der Polarebene auf, so gilt folgende Zuordnung zwischen den Koordinaten und elektrischen Größen :

Man bezieht alle Phasenlagen auf die Phasenlage der angelegten Spannung. Für den Momentanwert des Gesamtstromes gilt:

mit

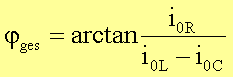
und

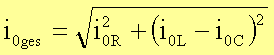
Bei Parallelschaltung von Wechselstromwiderständen werden wie im Gleichstromfall die Leitwerte addiert:

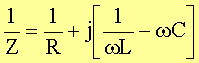
bzw.