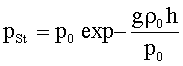Die Bernoulli-Gleichung

Bei Reibungsfreiheit gilt der Satz von der Erhaltung der mechanischen Energie:

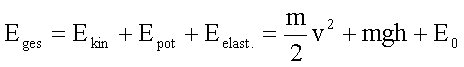
Indem wir die Energie auf die Volumeneinheit beziehen, gehen wir zu Energiedichte bzw. zu Drücken über:

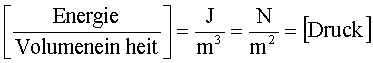
Die Energiebilanz geht dann über in die Bernoulligleichung

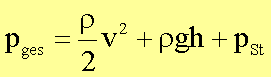
Der Gesamtdruck ergibt sich als Summe von Staudruck 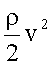, Schweredruck und statischem Druck p_St.

Ist die Dichte eine Funktion des Druckes, so gilt allgemeiner

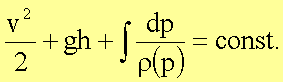
Für ein ideales Gas wird der Zusammenhang zwischen Druck und Dichte im isothermen Fall durch das Boyle’sche Gesetz beschrieben:

Das Boyle’sche Gesetz

Mit dem Molvolumen V_M und der molaren Masse µ erhält man

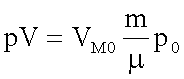
bzw.

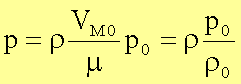
Unter Normalbedingungen (nicht Standardbedingungen) gilt:

T0	VM0	p0	r0(Luft)
0 °C = 273,15 K	22,4 l	1,01325^.10^5 Pa	1,29 kg / m^3

Für ein ideales Gas gilt: Bei gegebener Temperatur ist die Dichte eines Gases seinem Druck proportional.

Im folgenden interessieren wir uns für den Druck in einer nichtströmenden Flüssigkeits- bzw. Gassäule, d.h. mit v = 0 gilt:

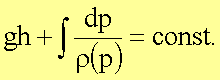
Für eine inkompressible Flüssigkeit mit p_ges (h=0) = p₀ gilt dann für den statischen Druck:

Der statische Druck einer Flüssigkeitssäule nimmt mit steigende Höhe ab.

Im Falle eines Gases gilt (in Näherung eines idealen Gases) bei konstanter Temperatur (isotherme Schichtung):

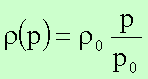
Die Berechnung des Integrals in der Bernoulli-Gleichung ergibt:

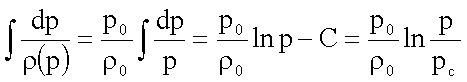
In der Höhe h = 0 sei der Druck p_ges = p_St = p₀ und die Dichte r₀. Daraus folgt für die Integrationskonstante p_c = p₀/e. Für die Höhenabhängigkeit des statischen Drucks ergibt sich die barometrische Höhenformel: