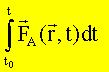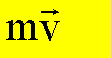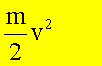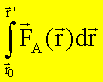Bewegungsintegrale – Abgeleitete Begriffe

Aus dem zweiten Newton’schen Axiom folgt ein dynamisches Kräftegleichgewicht zwischen der Summe der auf einen Körper der Masse m wirkenden äußeren Kräfte und der Trägheitskraft .

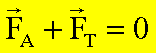
Ersetzt man die Trägheitskraft durch den Newton’schen Ausdruck, so folgt

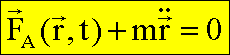
Diese Bewegungsgleichung ist eine Differentialgleichung zweiter Ordnung, d.h. die gesuchte Größe tritt in der zweiten Ableitung auf.

Integriert man die Bewegungsgleichung nach der Zeit, so gilt

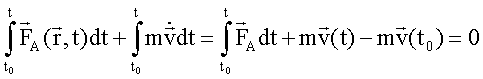
bzw.

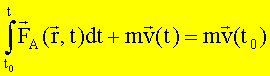
Die Summanden auf der linken Seite der Gleichung heißen

Kraftstoß:
Impuls:

Ist die Summe der äußeren Kräfte gleich Null, so ändert sich der Impuls nicht mit der Zeit, d.h. er ist eine Erhaltungsgröße.

Integriert man die Bewegungsgleichung nach dem Ort, so folgt

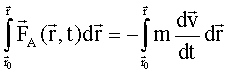
Gehen wir auf der rechten Seite zur neuen Integrationsvariablen dv über, so ist dies nur möglich, wenn auf der linken Seite der Gleichung keine zeit- und geschwindigkeitsabhängigen Größen stehen. In diesem Fall ist eine Trennung der Variablen (linke Seite: Integration über den Ort; rechte Seite: Integration über die Geschwindigkeit) möglich. Daher setzen wir im weiteren voraus, dass die Kraft nur vom Ort abhängt. Dann gilt:

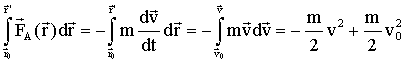
bzw.

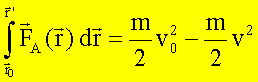
Die Größen auf der linken bzw. rechten Seite der Gleichung heißen:

Kinetische Energie:
Arbeit:

Wird ein Körper der Masse m im Raum gegen eine Kraft verschoben, so führt dies zu einer Änderung der kinetischen Energie.