Bewegung im Coulombfeld – Bohr’sche Bahnen

Kreisbahnen im Coulombfeld

Im folgenden betrachten wir die Bewegung eines Elektrons um eine positive Elementarladung. Dabei beschränken wir uns auf Kreisbahnen.

Im stationären Fall muss die Summe aus Coulombkraft (Zentripetalkraft) und Trägheitskraft (Zentrifugalkraft) verschwinden. Für ungleichnamige Ladungen ist die Coulombkraft negativ.

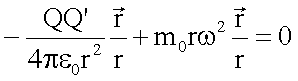
Damit erhält man in Analogie zum dritten Kepler’schen Gesetz einen Zusammenhang zwischen Bahnradius und Umlaufzeit (:

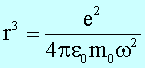
Wir benötigen eine weitere Bedingung, um Bahnradius und Umlaufzeit berechnen zu können. Kennt man den Drehimpuls

so hat man eine weitere Beziehung zwischen r und w, mit der die gesuchten Größen berechnet werden können. Bei der Beschreibung der Planetenbewegung ist faktisch jeder Wert für L denkbar. Geht man jedoch zu sehr kleinen Beträgen von L über, muss man berücksichtigen, dass der Drehimpuls gequantelt ist. Nach dem zweiten Bohr’schen Postulat genügt der Drehimpuls der Bedingung

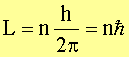
mit h als Planck’schem Wirkungsquantum und n als natürlicher Zahl. Mit n=1 existiert also ein kleinster Drehimpuls.

Mit

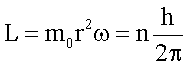
erhält man

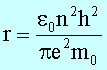
und

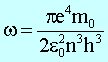
Energiezustände im Coulombfeld

Unter Verwendung der Ausdrücke für r und w können die Energiezustände der Elektronen berechnet werden. Die Gesamtenergie ergibt sich aus der Summe von kinetischer (Rotations-)Energie und potentieller Energie:

Mit

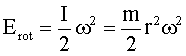
erhält man

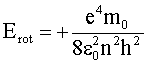
Das Potential einer positiven Elementarladung ist negativ:

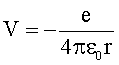
Durch Einsetzen von r folgt mit

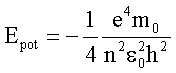
Für die Gesamtenergie folgt somit

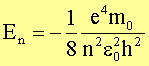
Übergänge zwischen Energiezuständen

Übergänge zwischen verschiedenen Energiezuständen E_n (mit n = n_A - Anfangszustand und n = n_E – Endzustand) können durch Absorption oder Emission von Lichtquanten der Energie hn und des Drehimpulses h/(2p) erfolgen. Dabei sind die Sätze von der Erhaltung der Energie und des Drehimpulses zu beachten:

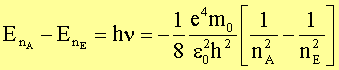
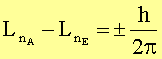bzw.

Die positiven Vorzeichen für die Energie- und Drehimpulsdifferenzen gelten für Emission von Lichtquanten, die negativen Vorzeichen für Absorption. Damit ist klar, dass die Frequenz der emittierten Lichtquanten n nichts zu tun hat mit der oben berechneten Umlauffrequenz w, wie dies ursprünglich vermutet worden war (siehe Thomson’sches Atommodell).