Das elektrische Feld eines Dipols

Feldlinien und Äquipotentiallinien eines Dipols

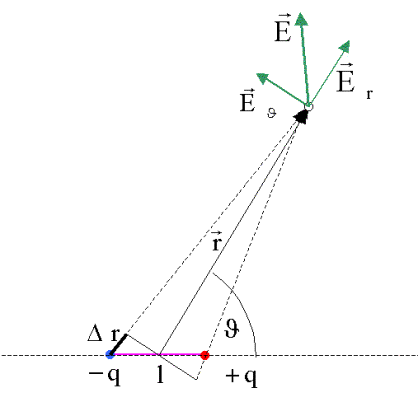
Wir interessieren uns für das vom Dipol erzeugte elektrische Feld im Aufpunkt mit den Koordinaten r und . Dabei sei vorausgesetzt, dass der Abstand der Dipolladungen l sehr klein gegen r sei. Das Feld berechnen wir aus dem Gradienten des Potentials. Das Potential ergibt sich durch Summation der Potentiale zweier Punktladungen:

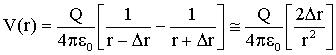
Hierbei wurde von der Tatsache Gebrauch gemacht, dass Dr²<<r².

Aus der letzten Skizze entnimmt man den Zusammenhang zwischen Dr und zu Damit erhält man für das Potential des Dipols in hinreichendem Abstand die Beziehung

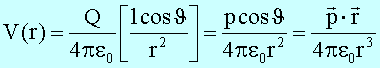
Das elektrische Feld erhält man aus dem Potential mittels der Relation .

In Kugelkoordinaten schreibt sich der Gradient folgendermaßen:

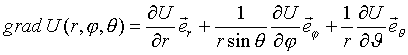
Da das Problem bezüglich des Winkels j rotationssymmetrisch ist und daher V auch nicht von j abhängt, erhält man das elektrische Feld mittels der Relation

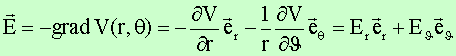
Die Radialkomponente des Feldes E_r ergibt sich zu

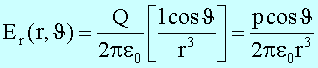
die Azimutalkomponente zu

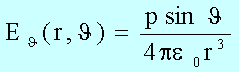
Den Betrag der Feldstärke erhält man mit zu

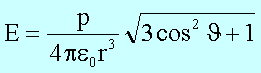
Der Betrag der Feldstärke nimmt mit der dritten Potenz des Abstandes vom Dipol ab. In Richtung der Dipolachse () ist die elektrische Feldstärke maximal, das Potential gleich Null. Senkrecht zur Dipolachse ist der Betrag der elektrischen Feldstärke minimal. In Richtung der Dipolachse trägt nur die Radialkomponente zum Feld bei, senkrecht dazu nur die Azimutalkomponente, die wegen der Drehung um 90° aber ebenfalls in Richtung der Dipolachse zeigt.