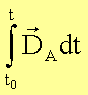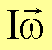Hauptträgheitsachsen, Stabilität und Drehimpuls bei der Rotation um freie Achsen

Das Massenträgheitsmoment eines Körpers hängt von der Lage der Rotationsachse ab. Wir betrachten einen Quader,

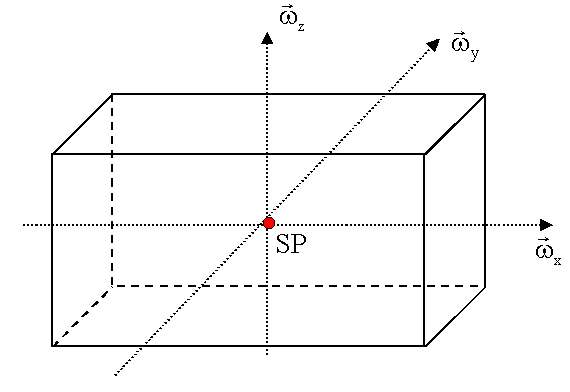
der um verschiedene Achsen durch den Schwerpunkt rotiert. Es zeigt sich, dass bei der Rotation des Körpers um seine Symmetrieachsen das Massenträgheitsmoment extremal wird. Trägt man I in Abhängigkeit von der Orientierung der Rotationsachsen bezüglich des körpereigenen Koordinatensystems (x,y,z) auf, so erhält man ein Ellipsoid:

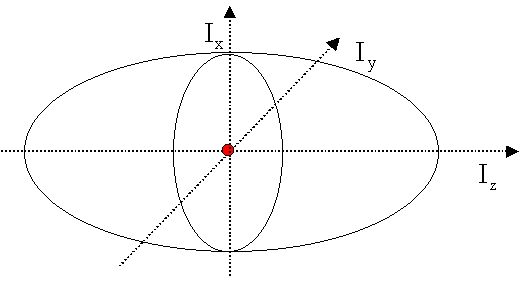
Mathematisch beschreibt man diese Eigenschaft durch den Trägheitstensor. Das ist im einfachsten Falle eine diagonale Matrix, die die Hauptträgheitsmomente enthält:

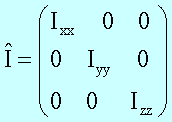
Die Bewegungsgleichung für rotierende Körper ändert sich dadurch nicht:

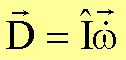
Die Beziehung zwischen den beiden Vektoren und wird jetzt jedoch durch einen Tensor vermittelt. Damit erhält man drei Gleichungen:

Die Komponenten entsprechen dabei den Komponenten der Winkelbeschleunigung um die Hauptträgheitsachsen.

Wir betrachten jetzt den Fall einer Rotation um eine Achse, die nicht mit der Hauptträgheitsachse zusammenfällt. An jedem Punkt des Körpers greifen Fliehkräfte an, die ein Drehmoment erzeugen, deren Summe den Körper u.U. in eine andere Position drehen. Der Körper befindet sich im stationären (weil er rotiert, sonst statisch) Gleichgewicht, wenn das resultierende Drehmoment verschwindet:

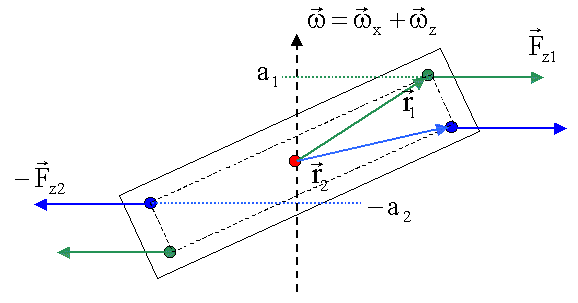
Das an den 4 gezeichneten Punkten angreifende resultierende Drehmoment ergibt sich zu

und bewirkt eine Drehung des Körpers um die y-Achse in die folgende Lage:

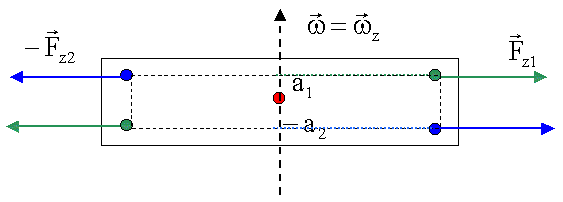
Wegen a₁ = a₂ und F_z1 = F_z2 gilt jetzt nach Summation der Drehmomente:

Diese Betrachtung kann für alle anderen Punkte des Quaders wiederholt werden.

Man gelangt zu dem Resultat, dass sich die Drehmomente bei der Rotation um symmetrische Achsen paarweise aufheben. Allgemein gilt für die 4 eingezeichneten Punkte:

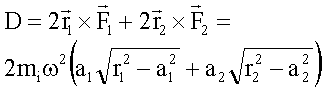
Hierin bedeuten a_i den senkrechten Abstand der Kraftwirkungslinie zum Drehpunkt und den Abstand des rotierenden Punktes zur Drehachse (für die Fliehkraft wirksamer Radius). In der symmetrischen Lage gilt a₁ = -a₂ und die Drehmomente der an gegenüberliegenden Punkten oberhalb und unterhalb des Schwerpunktes angreifenden Fliehkräfte heben sich paarweise auf. Dies gilt auch für die folgende symmetrische Position:

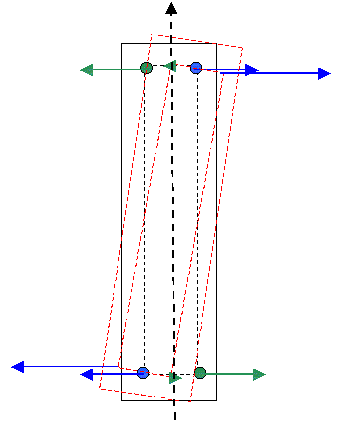
Ein geringes Abweichen aus der Gleichgewichtslage führt jedoch zu einem Drehmoment, welches den Körper in die oben diskutierte Position dreht. Daraus folgt zumindest im diskutierten Beispiel:

· Die Rotation um eine Hauptträgheitsachse ist eine Gleichgewichtslage.

· Die Rotation um die Hauptträgheitsachse mit dem maximalen Trägheitsmoment (hier z-Achse) ist stabil.

· Die Rotation um die Hauptträgheitsachse mit dem minimalen Massenträgheitsmoment ist instabil.

Rotiert ein Körper um eine instabile Achse, so wird er versuchen, in eine Position überzugehen, in der das Massenträgheitsmoment nicht nur extremal, sondern auch maximal ist. Dies ist natürlich nur möglich, wenn ihm hinreichend viel Energie zugeführt wird.

siehe Experiment in der Vorlesung

Ein stationäres Gleichgewicht liegt vor, wenn gilt:

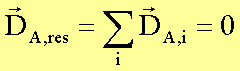
Das dynamische Gleichgewicht wird durch die Bewegungsgleichung für die Rotation beschrieben:

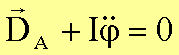
Sie führt auf ein neues Bewegungsintegral, den Drehimpuls. Mit

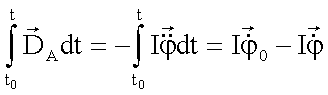
bzw.

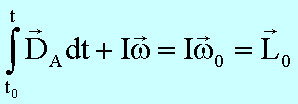
Mit dieser Gleichung definieren wir folgende Begriffe:

Drehstoß
Drehimpuls

Aus obiger Gleichung folgt :

Der Drehimpuls ist eine Erhaltungsgröße, wenn die

Summe aller äußeren Drehmomente gleich Null ist.

Daraus ergibt sich, dass im stationären Gleichgewicht eines rotierenden Körpers gilt:

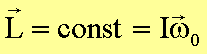
Für einen Massenpunkt erhält man mit I = mr² hieraus den Drehimpuls

Ist der Impuls eines Massenpunktes sowie sein Ortsvektor gegeben, so ist der Drehimpuls durch

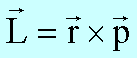
gegeben. Hieraus folgt sofort wieder , wenn r_a dem Abstand der Masse zur Drehachse entspricht.