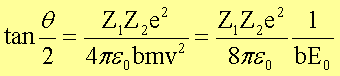Drehimpulserhaltung
Drehimpulserhaltung im Zentralfeld
Im Fall des Gravitationspotentials (Planetenbewegung) oder des Coulombpotentials (Rutherfordstreuung) bewegt sich eine Masse m unter dem Einfluss einer Zentralkraft
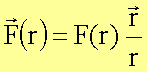
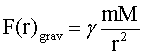
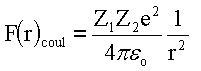
Im Falle einer Zentralkraft (z.B. Gravitationskraft, Coulombkraft) hängt der Betrag der Kraft nur vom Abstand r zum Kraftzentrum ab. Der Zusammenhang zwischen Kraft und Potential kann folgendermaßen geschrieben werden:
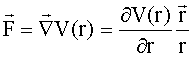
Mit
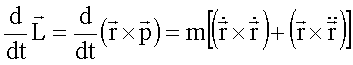
gilt unter Beachtung der Tatsache, dass das Kreuzprodukt
paralleler Vektoren verschwindet:
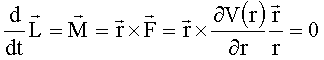
Der Drehimpuls des Projektils bleibt erhalten, da kein
äußeres Drehmoment auf das Projektil einwirkt. Da die Richtung einer
Zentralkraft parallel zum Ortsvektor 
wirkt, ist das
Kreuzprodukt und damit das Drehmoment gleich Null, d.h. der Drehimpuls ist eine
(Bewegungs)konstante.
Aus der Drehimpulserhaltung folgt sofort der Flächensatz (2. Kepler’sches Gesetz) für Kegelschnittbahnen (1. Keplergesetz):
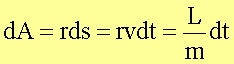
Drehimpulserhaltung bei der Rutherfordstreuung
Im Fall der Rutherfordstreuung bewegt sich das Projektil unter dem Einfluss einer Zentralkraft
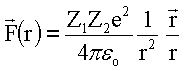
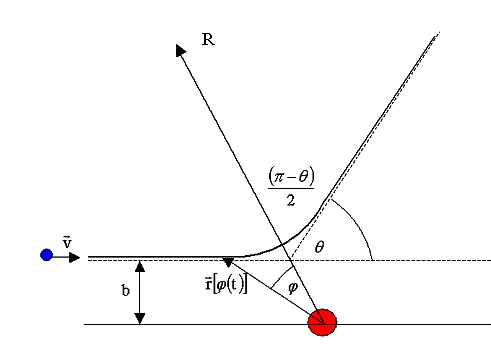
Der Drehimpuls des Projektils (Punktmasse m) kann mittels folgender Gleichungen ausgedrückt werden:
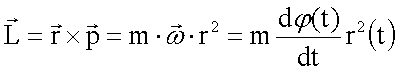
Der Anfangsdrehimpuls ist gegeben durch (b – Stoßparameter)
Unter Verwendung der ersten Gleichung erhalten wir über
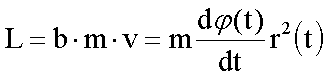
die
Winkelgeschwindigkeit
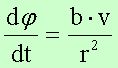
Für
die (Linear)Impulskomponente des Projektils in Richtung der Achse R (in großer
Entfernung vom Targetatom) gilt 
. Damit erhält man für die Impulsänderung (gleich dem Kraftstoß):
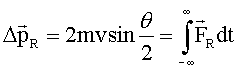
Der
in radialer Richtung wirkenden Kraft entspricht hier die Coulombkraft 
. Wir betrachten hier die Kraftkomponente in Richtung R, d.h.
FR = F.cosj. Somit folgt für die Impulsänderung:
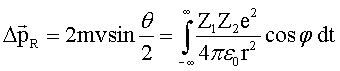
Wir
substituieren dt durch dj mittels 
:
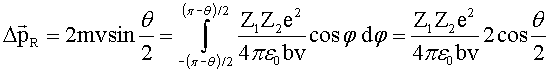
und
somit für den Ablenkwinkel 
