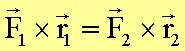Das Drehmoment

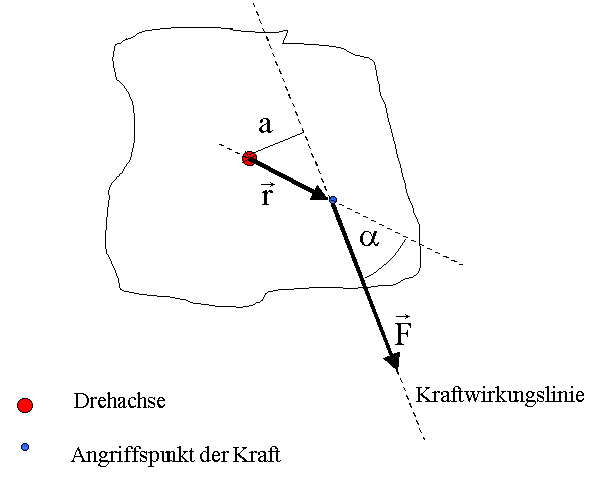
Der Betrag des Drehmoment D ist definiert als das Produkt aus dem Betrag der Kraft und dem senkrechten Abstand a der Kraftwirkungslinie zum Drehpunkt:

Die Richtung des Drehmomentes ergibt sich aus der Lage der Drehachse, steht also senkrecht auf und . Damit ist das Drehmoment allgemein als Vektorprodukt aus Abstandsvektor und Kraft anzugeben:

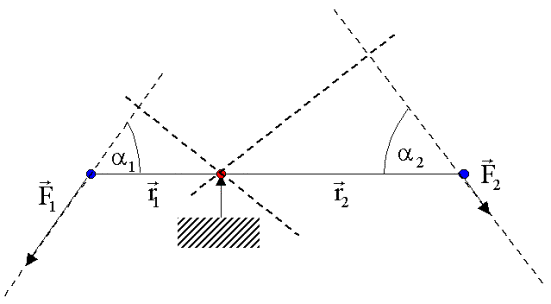
Das Drehmoment wird benötigt, um eine Rotationsbewegung zu beschreiben. Verläuft die Kraftwirkungslinie durch den Drehpunkt, so findet keine Rotation statt ( sina = 0 ). Steht die Kraft senkrecht auf dem Radiusvektor, so ist der Antrieb am wirkungsvollsten.

Greifen mehrere Kräfte an verschiedenen Stellen an, so addieren sich die Drehmomente vektoriell:

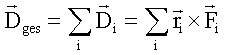
Eine Rotation findet nicht statt, wenn die Summe aller angreifenden Drehmomente verschwindet (Drehmomentensatz)

Ein Körper ist bezüglich der Rotation im Gleichgewicht, wenn die Summe aller angreifenden Drehmomente verschwindet.

vergleiche Translation:

Ein Körper ist bezüglich einer Translation im Gleichgewicht, wenn die Summe aller angreifenden Kräfte verschwindet.

Wird ein Körper im Schwerefeld der Erde aufgehängt, so greift an jedem Masseelement dm die Schwerkraft gdm an. Das gesamte wirksame Drehmoment ergibt sich zu:

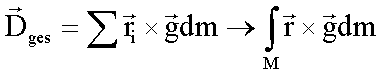
Da g ein konstanter Faktor ist, kann man ihn (unter Berücksichtigung der Vertauschungsregel im Vektorprodukt) vor das Integral ziehen:

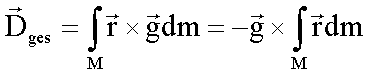
Mit der Definition des Schwerpunktes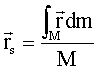

lässt sich das gesamte Drehmoment ausdrücken durch

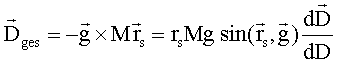
Das gesamte Drehmoment ergibt sich aus dem Kreuzprodukt von Gewicht und einem Ortsvektor, der von der Drehachse zum Schwerpunkt weist.

Ein im Schwerefeld der Erde drehbar aufgehängter Körper verhält sich so, als würde sein gesamtes Gewicht im Schwerpunkt angreifen. Wird ein Körper direkt im Schwerpunkt drehbar gelagert, ist das resultierende Drehmoment gleich Null. In diesem Falle erfolgt in keiner Position eine Drehung unter dem Einfluß der Schwerkraft – der Körper ist stabil gelagert.

Das Hebelgesetz

Eine einfache Anwendung findet der Drehmomentensatz beim zweiarmigen Hebel (z.B. Balkenwaage):