Der Energiesatz der Mechanik

Wir gehen davon aus, dass sich ein Kraftfeld durch ein Potential ausdrücken lässt. Dies ist dann der Fall, wenn das Potential nur vom Ort abhängt und nicht von dem Weg, auf dem ein Massenpunkt dorthin gebracht wird. Solche Kraftfelder, z.B. das Gravitationsfeld, nennt man konservativ (wie wir sehen werden, weil sie die mechanische Energie erhalten). Es muss also gelten:

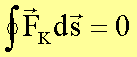
Mittels der allgemein geltenden Vektoridentitäten

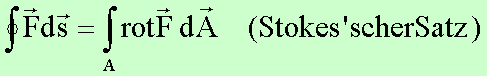
und

folgt sofort auch formal mathematisch, dass die Kraft aus einem Potential abgeleitet werden kann, wenn das geschlossene Wegintegral über der Kraft gleich Null ist:

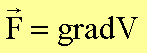
Für die Reibungskraft gilt dagegen:

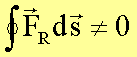
Es ist sofort einzusehen, dass die Reibungsarbeit nicht verschwindet, wenn man auf einem geschlossenen Kreis fährt. Hier wird mechanische Energie in Wärme verwandelt, ist also keine Erhaltungsgröße (Dies ist keine Aussage über die allgemeine Energieerhaltung).

Die Kraft lässt sich aus einem Potential ableiten, wenn sie nur vom Ort abhängt. Kräfte, die nur vom Ort abhängen, heißen konservative Kräfte. Kräfte, die von der Zeit bzw. der Geschwindigkeit abhängen, sind keine Potentialkräfte.

Für konservative Kräfte gilt mit

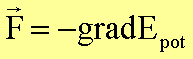
und

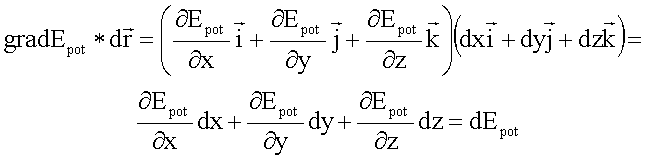
auch

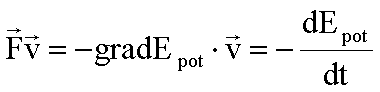
Außerdem gilt

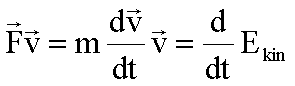
Durch Vergleich erhält man:

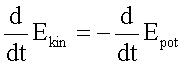
bzw.

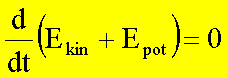
Wenn die totale zeitliche Ableitung einer Größe Null ist, so ist sie eine Erhaltungsgröße. Die letzte Gleichung drückt somit die Erhaltung der mechanischen Energie aus, sofern die wirkenden Kräfte konservativ sind: