Freier Fall um die Erde

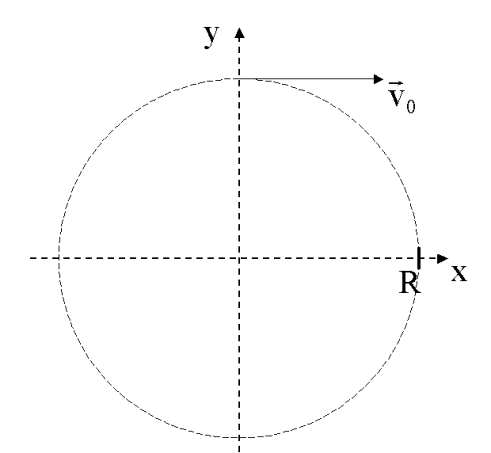
Erdradius: R = 6378 km ; g(R) = 9,81 m/s²

Wir werfen einen Körper nahe der Erdoberfläche mit einer solchen Geschwindigkeit, dass der Krümmungsradius in jedem Punkt der Bahn gleich dem Erdradius ist. Für den waagerechten Wurf gilt:

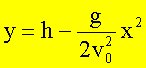
Mit der Beziehung für den Krümmungsradius

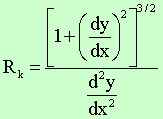
folgt unter Ausnutzung von

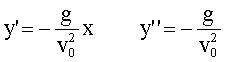
an der Stelle x = 0 der Krümmungsradius

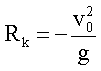
bzw. die nötige Geschwindigkeit für R_k = -R zu

Da man diese Betrachtung für jeden folgenden Teil der Bahn wiederholen kann, bewegt sich ein Körper auf einer Kreisbahn mit

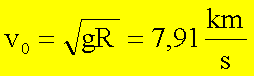
nahe der Erdoberfläche.

newtonberg.html

Eine einfachere Berechnungsmethode für diese erste kosmische Geschwindigkeit basiert auf der Kinematik der Kreisbewegung:

Aus der Gleichheit von Gravitationsbeschleunigung g und Zentripetalbeschleunigung v²/R erhält man ebenfalls:

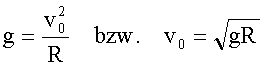
Wir vergleichen diese Geschwindigkeit mit der thermischen Geschwindigkeit eines Gasmoleküls. Die kinetische Gastheorie liefert aus der Gleichheit von kinetischer Energie und thermischer Translationsenergie:

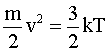
die Geschwindigkeit

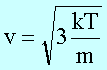
Boltzmannkonstante k = 1,38^.10^-23 JK^-1

Für ein Stickstoffmolekül mit m = 28 m_H ; m_H = 1,67^.10^-27 kg

erhält man bei der Temperatur 300 K eine mittlere Geschwindigkeit von 515 m/s. Leichtere Gase sind etwas schneller, ein Wasserstoffmolekül bringt es auf fast 2 km /s. Diese Geschwindigkeiten sind viel kleiner, als die erste kosmische Geschwindigkeit und erst recht kleiner, als die zweite kosmische Geschwindigkeit (Entweichgeschwindigkeit von der Erde).

Für den Mond (g = 1,67 m/s² ; R = 1738 km) erhalten wir dagegen eine Kreisbahngeschwindigkeit von nur 1,7 km/s. Der Mond ist also kaum in der Lage, eine Atmosphäre über längere Zeit zu halten. Da die angegebenen Gasgeschwindigkeiten nur mittlere Geschwindigkeiten sind, finden sich immer einige Moleküle mit hinreichender Geschwindigkeit, die in der Lage sind, sich von der Oberfläche zu entfernen.