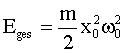Freie, ungedämpfte, harmonische Schwingungen
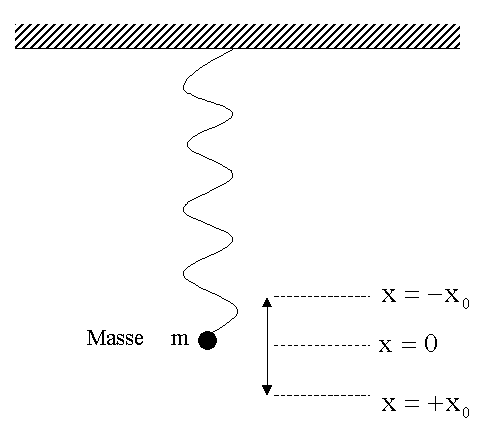
Im
Falle des Federschwingers führt die Masse m eine zeitlich periodische
Bewegung um die Ruhelage x = a aus, wenn sie zuvor um den Betrag x0
(Amplitude) aus der Ruhelage ausgelenkt wurde. Die Periodendauer
T (reziproke Frequenz) ist bestimmt durch das Gleichgewicht aus
Trägheitskraft und Rückstellkraft der Feder und hängt damit von der Masse und
der Rückstellkraft der Feder ab. Aus der Bewegungsgleichung
![]()
erhält
man die Auslenkung (Elongation) x mit ![]() zu
zu
![]()
Eine solche Lösung erhält man generell, wenn die Kraft linear von x bzw. das Potential der Kraft quadratisch von x abhängt. Ein vom Ort quadratisch abhängendes Potential nennt man auch harmonisch, da es die Ursache für harmonische (sinusförmige) Schwingungen ist.
|
harmonisches Potential |
|
|
harmonische Schwingung |
|
Elongation |
|
Amplitude |
|
Kreisfrequenz ; Frequenz |
|
Phasenwinkel |
|
Phase |
|
Gesamtenergie |
|
Im Falle einer ungedämpften Schwingung gilt der Satz von der Erhaltung der mechanischen Energie. Im oben angeführten Beispiel kann die Schwingungsgleichung direkt aus der Energieerhaltung abgeleitet werden:
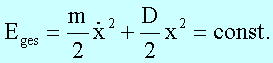
Durch Differenzieren nach der Zeit erhält man:
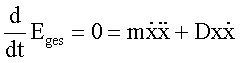
bzw.
![]()
oder
![]()
Im Falle einer ungedämpften harmonischen Schwingung ist die mechanische Gesamtenergie eine Erhaltungsgröße. Es findet eine periodische Umwandlung von kinetischer in potentielle Energie statt. Mit
![]() und
und ![]()
erhält
man durch Einsetzen in 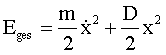 für die Gesamtenergie:
für die Gesamtenergie:
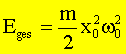
d.h.
für den Federschwinger mit ![]() :
:
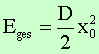
und
für das mathematische Pendel mit ![]() und
und ![]() :
:
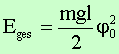
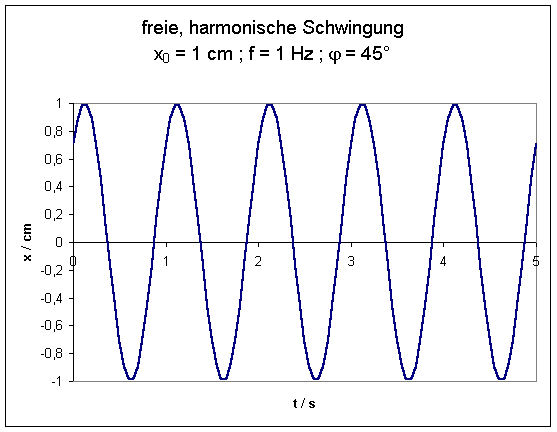
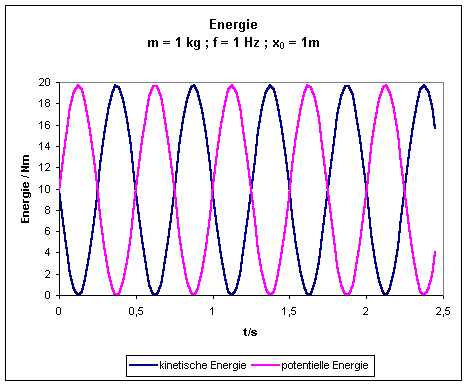
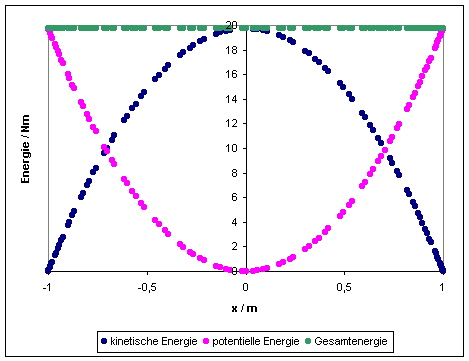
In
den folgenden beiden grafischen Darstellungen ist für die Parameter m = 1 kg, f
= 1 Hz (bzw. w0 = 6,28.. s-1), x0
= 1m die kinetische und potentielle Energie in Abhängigkeit von der Zeit sowie
von der Auslenkung x dargestellt:
Viele Potentiale, die einen Schwingungsvorgang verursachen, sind nicht harmonisch. In der Nähe eines Potentialminimums kann ein nichtharmonisches Potential jedoch meistens durch eine Parabel angenähert werden. Für kleine Abweichungen aus der Ruhelage ist dann ein solcher Schwingungsvorgang harmonisch – siehe z.B. das Lenard-Jones-Potential:
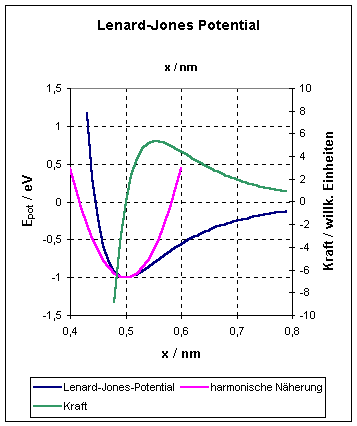
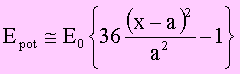
Das LJP ist quadratisch in den Koordinaten und führt auf eine oszillierende Bewegung um die Gleichgewichtslage x = a mit der Frequenz
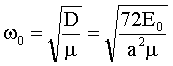
wobei
µ die reduzierte Masse der beiden wechselwirkenden Massenpunkte darstellt
(siehe später – Rotation starrer Körper).