Freie gedämpfte Schwingungen

Reale Schwingungsvorgänge verlaufen gedämpft, da mechanische Energie in andere Energieformen umgewandelt wird. Meistens sind es Reibungsvorgänge, bei denen Bewegungsenergie in Wärme verwandelt wird.

Wir wollen annehmen, dass die Reibung wie im Falle der Stokes’schen Reibung vom Betrag der Geschwindigkeit abhängt und setzen die Reibungskraft (r_k – Reibungskoeffizient) an mit

Des weiteren wirke eine rücktreibende Kraft, die einen ausgelenkten Oszillator in seine Ruhestellung zurücktreibt. Diese Kraft sei wie im Falle des Federschwingers oder des mathematischen Pendels eine lineare Funktion des Ortes:

Die Bewegungsgleichung unter Einbeziehung der Trägheitskraft lautet dann:

Im eindimensionalen Fall (hier sei ) vereinfacht sich die letzte Gleichung zu

Dies ist die Bewegungsgleichung des linearen gedämpften harmonischen Oszillators.

Mit den Abkürzungen

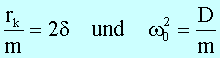
lautet die Gleichung

Diese homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten kann mit folgendem Ansatz gelöst werden:

Mit 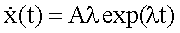und 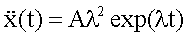erhält man durch Einsetzen in die Differentialgleichung (Dgl) eine quadratische Gleichung für den Parameter l:

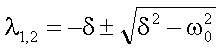
Die Lösung der Dgl kann als Linearkombination unter Verwendung des Lösungsansatzes für beide Parameter geschrieben werden:

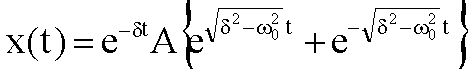
Wir diskutieren die Lösung dieser Gleichung in drei Fällen:

schwache Dämpfung	Schwingfall
	Aperiodischer Grenzfall
starke Dämpfung	Kriechfall

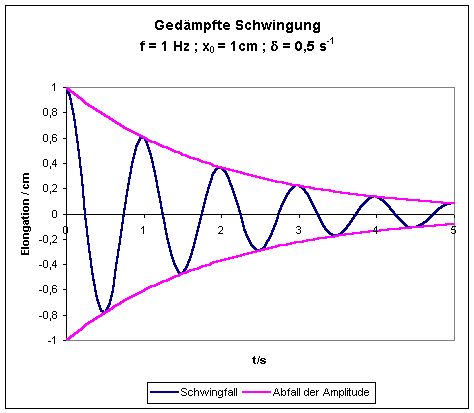
Der Schwingfall

Im Falle schwacher Dämpfung ist . Damit führt die Wurzel aus einer negativen Zahl zu einem komplexen Ausdruck. Unter Verwendung des Ausdruckes für eine komplexe Exponentialfunktion

(i imaginäre Einheit: ) vereinfacht sich der obere Ausdruck zu

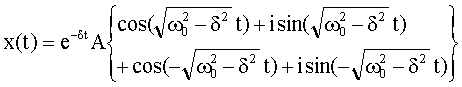
Mit sin-x = -sinx und cos-x =cosx gilt dann

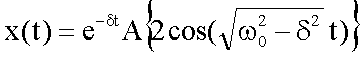
Mir der neuen Amplitude x₀ = 2A erhalten wir schließlich

Diese Gleichung beschreibt eine Schwingung mit der Kreisfrequenz

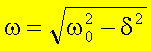
deren Amplitude exponentiell mit der Zeit abnimt. Den Parameter , der die Stärke des Abfalls mit der Zeit beschreibt, nennt man auch logarithmisches Dekrement.

Der Kriechfall

Im Fall starker Dämpfung erhalten wir mit

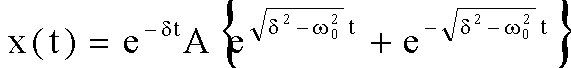
unter Verwendung der Beziehung 2sinh(z)=exp(z)-exp(-z) :

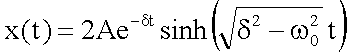
Ersetzt man wieder 2A durch die Amplitude x₀, so gilt schließlich

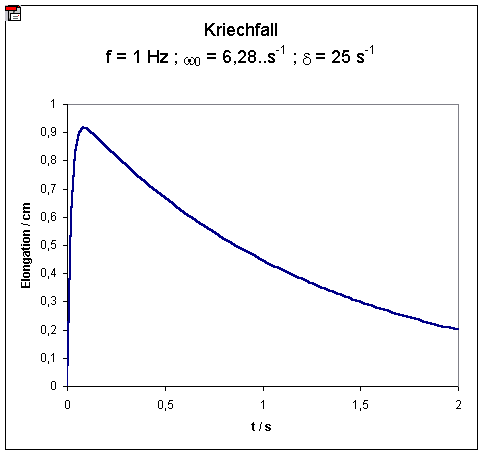
Nach einem kurzen Anstieg fällt die Amplitude mit einer durch die Dämpfung d bestimmten Zeitkonstante ab:

Aperiodischer Grenzfall

Der aperiodische Grenzfall ist gegeben unter der Bedingung .

Mit einem veränderten Lösungsansatz erhält man als Lösung der Bewegungsgleichung

Die Funktion x(t) verläuft ähnlich wie im Kriechfall, geht jedoch in der kürzestmöglichen Zeit gegen Null.

Beispiel

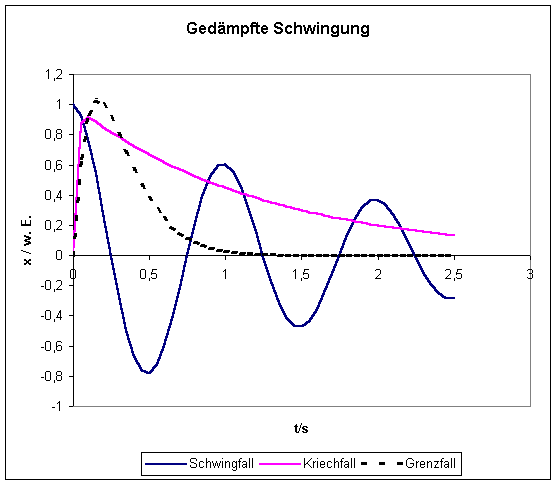
Die oben gezeigten Funktionen wurden für folgende Parameter berechnet:

Frequenz der ungedämpften Schwingung: f = 1 Hz

Schwingfall: d = 0,5 s^-1 ; d^-1 = t = 2 s

Kriechfall: d = 30 s^-1

Aperiodischer Grenzfall: d = w₀ = 2pf = 6,28...s^-1