Die geradlinig gleichförmige Bewegung

Wir haben eine bezüglich Betrag und Richtung zeitlich konstante Geschwindigkeit:

Die Beschleunigung ist daher gleich Null:

Das Weg – Zeit - Gesetz der geradlinig gleichförmigen Bewegung ergibt sich mittels

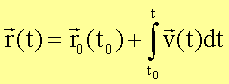
zu

Da die Größen , und , Vektoren sind, erhält man mit

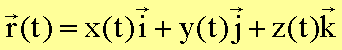
und

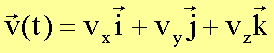
aus obiger Vektorgleichung drei Gleichungen:

Galileitransformation und

Additionstheorem der Geschwindigkeiten

Koordinatensysteme, die sich relativ zueinander mit geradlinig gleichförmiger Geschwindigkeit v_r bewegen, heißen Inertialsysteme. Für diese Systeme gilt im Rahmen der klassischen Mechanik beim Übergang von einem Koordinatensystem in ein anderes Bezugssystem die Galileitransformation sowie das Additionstheorem der Geschwindigkeiten.

Es seien A und B zwei Systeme, die sich relativ zueinander mit der konstanten Geschwindigkeit v_r bewegen.

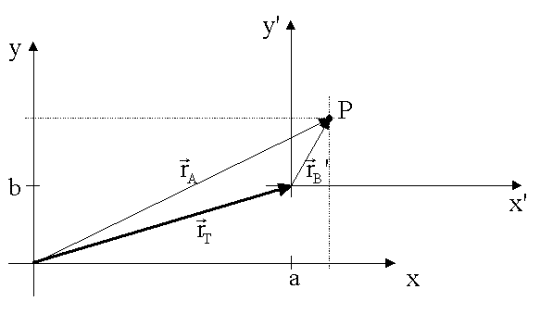
Im System A (ungestrichenes System) seien die Koordinaten des Ortsvektors r mit (x,y,z) bezeichnet.

Im System B (gestrichenes System) seien die Koordinaten des Ortsvektors r’ mit (x’,y’,z’) bezeichnet.

Die Position eines Massenpunktes lässt sich zwischen B und A folgendermaßen umrechnen:

Galileitransformation:

Ein Massenpunkt, der bezüglich B die Geschwindigkeit u’ hat, bewegt sich bezüglich A mit der Geschwindigkeit

Additionstheorem: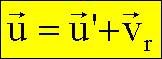

Das Additionstheorem folgt sofort aus der Galileitransformation durch Differentiation mit

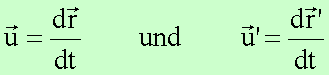
Es wird deutlich, dass dies so nur gilt, wenn die Zeit t keiner Transformation unterliegt, d.h. t = t’.

Für die Beschleunigung, die Kraft und die Zeit ergeben sich beim Übergang von A nach B keine Änderungen, d.h. es gilt:

a = a’ ; F = F’ ; t = t’

In Nichtinertialsystemen ( beschleunigten Bezugssystemen ) treten zusätzliche Kräfte, sogenannte Trägheitskräfte auf (Beispiel: Fliehkraft).