Impulserhaltung und Massenschwerpunkt

Es gilt die Newton’sche Bewegungsgleichung in der Form

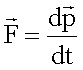
Greifen mehrere Kräfte n an einem abgeschlossenen System an, das aus mehreren Teilchen N besteht, so gilt:

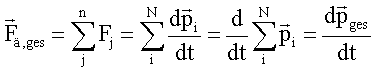
Die Wechselwirkung der Teilchen untereinander wurde in obiger Gleichung nicht berücksichtigt, da sich paarweise auftretende innere Kräfte wegen des Prinzips actio = reactio aufheben. Damit ist für die Impulsänderung eines Teilchensystems nur die Summe der äußeren Kräfte relevant. Ist die Summe der äußeren Kräfte gleich Null, so gilt mit

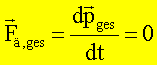
auch

Der Gesamtimpuls eines abgeschlossenen Systems von N Teilchen ist eine Erhaltungsgröße, wenn die Summe der äußeren am System angreifenden Kräfte verschwindet.

Wir betrachten nun ein System von N Teilchen der Masse m_i und der Gesamtmasse M mit den jeweiligen Koordinaten . Der Schwerpunkt dieses Systems ist gegeben durch

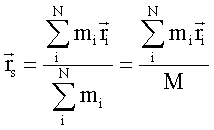
bzw.

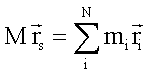
Der Impuls des Massenschwerpunktes ergibt sich durch Differentiation nach der Zeit zu

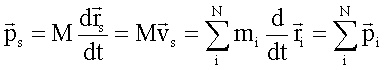
Der Impuls des Massenschwerpunktes ist gleich der Summe der Einzelimpulse.

Auf diesem Satz beruht die Punktmassenmechanik. Die Bewegung eines Systems von Teilchen (z.B. eines Körpers) lässt sich behandeln als die Bewegung der im Schwerpunkt vereinigten Gesamtmasse des Körpers.

Begibt man sich in ein Koordinatensystem, das mit dem Massenschwerpunkt verbunden ist, so ist . Daraus folgt:

Die Summe aller Impulse im Schwerpunktsystem ist immer Null.