Koordinatensysteme

Kartesische Koordinaten

 

 

 

 

 

 

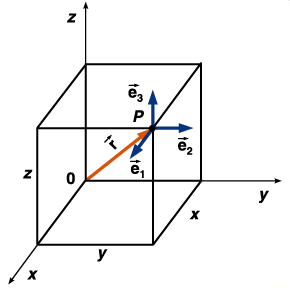
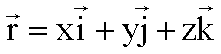
Betrag des Ortsvektors:

 

 

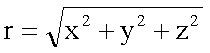
Abstand zwischen zwei Punkten (x2,y2,z2) und (x1,y1,z1):

 

 

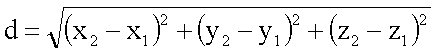
Volumenelement:



Zylinderkoordinaten

 

 

(in der Ebene Polarkoordinaten)

 

 

 

 

 

 

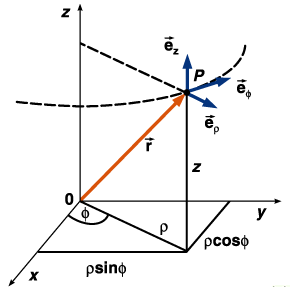
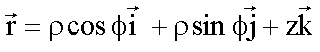
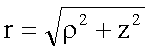
Abstand zwischen zwei Punkten (r2,f2,z2) und (r1,f1,z1):

 

 

Volumenelement:

 

 

 

 

 

 

 

Kugelkoordinaten

 

 

 

 

 

 

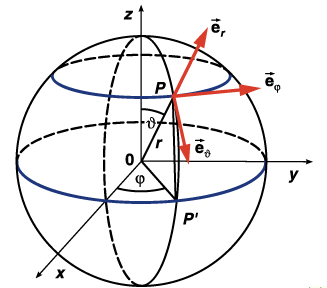
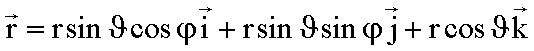
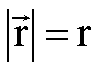
Zylinderkoordinaten können folgendermaßen in Kugelkoordinaten umgerechnet werden:

                                                                                                                             

                                

 

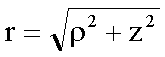
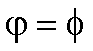
Volumenelement:

 

Koordinatentransformationen

 

Es seien (x,y,z) die Koordinaten eines beliebigen Punktes bezüglich eines Koordinatensystems A. Wir interessieren uns für die Koordinaten (x’,y’,z’) dieses Punktes, nachdem er um einen Vektor  verschoben bzw./und um eine vorgegebene Achse gedreht wurde.

 

Translation

 

Der Punkt (x,y,z) werde um den Vektor  von der Position P auf die Position P’ verschoben. Dann gilt für die neuen Koordinaten (x’,y’,z’) des Punktes an der Position P’:

 

 

Im einzelnen haben wir dann:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 





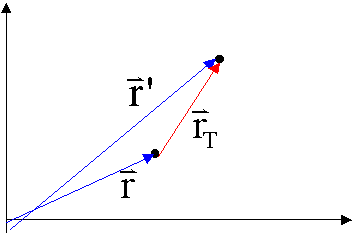
Rotation

 

Der Punkt P soll um den Winkel fD verdreht werden. Wir wählen als Rotationsachse die z-Achse. Allgemein können die Koordinaten eines Punktes bezüglich der gegeneinander verdrehten Systeme durch eine Gleichung der Form

 

 

ineinander überführt werden. Hier ist die Transformationsmatrix, welche die Koordinaten eines Punktes bezüglich des ruhenden Systems A vor der Drehung in die Koordinaten nach der Drehung transformiert. Für die Berechnung der neuen Koordinaten  aus den alten gilt:

 

 

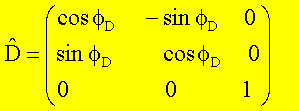
Ausmultipliziert erhalten wir:

 

 

In Zylinderkoordinaten gilt einfacher:

 

 

Umgekehrt kann man natürlich auch den Übergang von 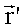 nach 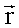  berechnen, wenn die Koordinaten bezüglich des verdrehten Systems B bekannt sind:

 

 

 

Für D’ gilt dann:

 

 

 

 

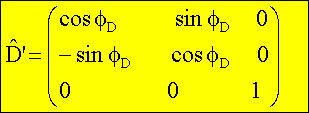
Zusammengesetzte Transformationen


Im allgemeinen Fall kann eine Transformation in eine Translation und eine Drehung zerlegt werden.

Aufeinanderfolgende Koordinatentransformationen sind i.a. in der Reihenfolge durchzuführen, wie sie stattgefunden haben. Insbesondere dürfen mehrere Drehungen nicht in ihrer Reihenfolge vertauscht werden.

 

Wird ein Punkt zuerst um die z-Achse verdreht und dann verschoben, so erhält man:

 

 

Wird der Punkt P zuerst verschoben und danach um die z-Achse gedreht, so gilt:

 

 

Wenn sich ein Punkt P bewegt, ändern sich die Größen fD  und  mit der Zeit.