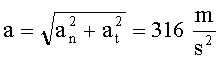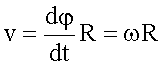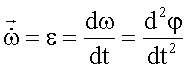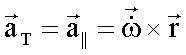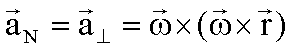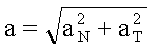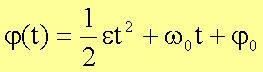Kreisbewegung

Bahnkurve
|
Kartesische
Koordinaten |
|
|
|
Polarkoordinaten |
Radius |
|
|
Bahnlänge |
||
|
|
|
|
Bahn(Tangential)geschwindigkeit
|
Kartesische
Koordinaten |
|
|
Polarkoordinaten |
|
|
|
|
Winkelgeschwindigkeit
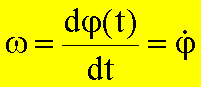
Maßeinheit: rad.s-1
Der Vektor der Winkelgeschwindigkeit ist parallel zur Rotationsachse (axialer Vektor) und senkrecht zur Bahnebene gerichtet. Er steht damit senkrecht auf dem Radiusvektor und senkrecht zum Vektor der Tangentialgeschwindigkeit. Anschaulich kann seine Richtung durch die Bewegungsrichtung einer Schraube mit Rechtsgewinde beschrieben werden. Die rechte Daumen-Regel gilt analog.
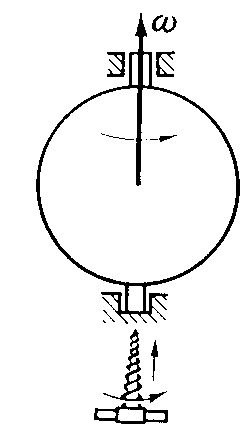
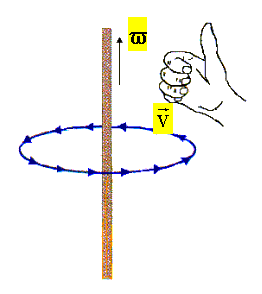
Die Winkelgeschwindigkeit w (Winkeldifferenz pro Zeiteinheit) heißt auch
Kreisfrequenz. Sie kann aus der Frequenz f (Umdrehungen pro Zeiteinheit) mittels ![]() berechnet werden.
berechnet werden.
Der Zusammenhang zwischen Winkelgeschwindigkeit, Bahngeschwindigkeit und Radiusvektor wird durch die Eulergleichung beschrieben:
Eulergleichung
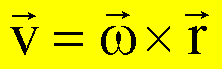
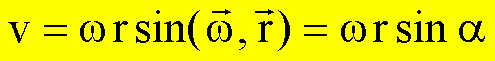
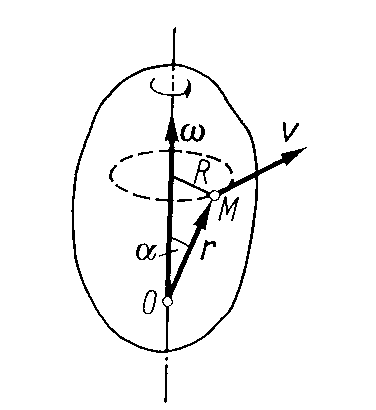
Diskussion der Eulergleichung
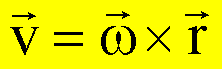
Die Beschleunigung erhält man aus der ersten Ableitung der Geschwindigkeit nach der Zeit:
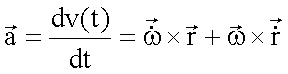
Einsetzen
der Eulerbeziehung für ![]() ergibt für die
Gesamt- oder Linearbeschleunigung:
ergibt für die
Gesamt- oder Linearbeschleunigung:
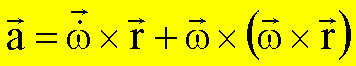
Die einzelnen Größen haben folgende Bedeutung:
|
Winkelbeschleunigung |
|
|
Tangential- oder Azimutalbeschleunigung |
|
|
Normal-, Radial- oder Zentripetalbeschleunigung |
|
|
Gesamtbeschleunigung |
|
Die oberen Gleichungen gelten unter der
Voraussetzung, dass ein Massenpunkt im rotierenden Bezugssystem ruht.
In der folgenden Grafik sind die einzelnen
Komponenten der Beschleunigung dargestellt:

Der Betrag der Gesamtbeschleunigung ergibt sich damit
zu
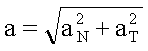
Auch für aT = 0
ist die Normalbeschleunigung ungleich Null. Die Kreisbewegung ist also immer
eine beschleunigte Bewegung.
Kreisbewegung
mit Tangentialbeschleunigung = 0
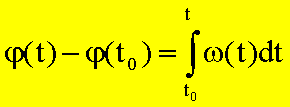
Wegen vT = const. Und w(t) = w = const. folgt:
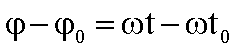
Für einen vollen Umlauf gilt: ![]()
und damit 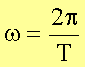
bzw. mit der Frequenz
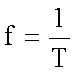
auch
![]()
Die Kreisbewegung mit konstanter Bahngeschwindigkeit
v = wR ist eine beschleunigte Bewegung. Um die
Kreisbewegung aufrecht zu erhalten, muss eine zum Zentrum hin gerichtete Kraft
aufgewandt werden – die Zentripetalkraft. Für den Betrag der Zentripetalkraft
gilt (siehe oben):
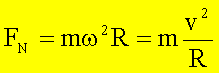
Da sich die Richtung der Kraft laufend ändert, ist die Kreisbewegung eine ungleichmäßig beschleunigte Bewegung.
Die Kreisbewegung mit
konstanter
Tangentialbschleunigung
Spricht man von der gleichmäßig beschleunigten Kreisbewegung, so ist damit eine Kreisbewegung mit konstanter Winkelbeschleunigung gemeint. Wie oben bereits diskutiert wurde, ist bereits die gleichförmige Kreisbewegung ungleichmäßig beschleunigt.
Aus
![]()
folgt
mit
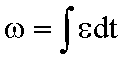
die Winkelgeschwindigkeit
![]()
Weiterhin erhält man mit
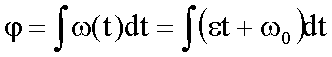
Die
Radialgeschwindigkeit ist gleich Null, die Radialbeschleunigung ist gleich der
Zentripetalbeschleunigung.
Beispiel Hammerwerfer
Eine Masse von m = 7,2 kg werde auf einem Radius von
R = 2m gleichmäßig beschleunigt und unter dem Winkel j = 45° (maximale Reichweite) zur Vertikalen
losgelassen. Die maximale Rotationsfrequenz von fmax = 2s-1
wird nach n = 3 Umdrehungen erreicht.
· Bahngeschwindigkeit und
Wurfweite
Die maximale momentane Bahngeschwindigkeit wird nach 3 Umdrehungen am Ende der
Beschleunigungsphase erreicht:
![]()
Die erreichbare Wurfweite
beträgt somit
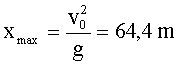
· Normalbeschleunigung und
Zentripetalkraft
Die maximale Radialbeschleunigung folgt aus
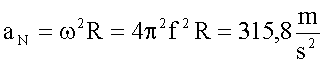
Die maximal aufzuwendende
Normalkraftkomponente, um die Masse auf der Kreisbahn zu halten, beträgt damit
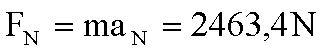
· Winkel-, Bahn- und
Gesamtbeschleunigung
Voraussetzung: ![]() Þ
Þ
![]()
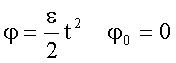
Eliminiert man aus den beiden letzten
Gleichungen t, so folgt:
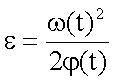
Am Ende der Beschleunigungsphase
erhält man mit
![]()
eine Winkelbeschleunigung von
![]()
Daraus folgt eine
Tangentialbeschleunigung von
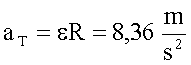
Damit folgt eine Gesamtbeschleunigung
von