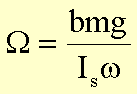Präzession eines Kreisels

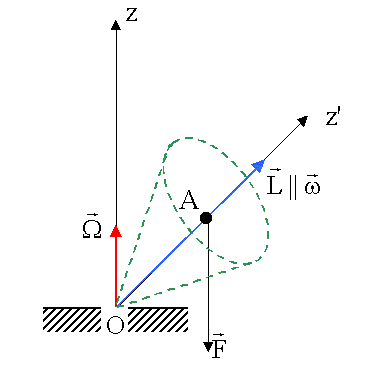
Als symmetrischen Kreisel bezeichnet man einen starren Körper, der um einen festen Punkt O rotiert und eine dynamische Symmetrieachse (z’-Achse) besitzt, die durch seinen Schwerpunkt geht. Fällt der Punkt O mit dem Schwerpunkt des Kreisels zusammen, so ist der Kreisel kräftefrei im Gravitationsfeld. Anderenfalls spricht man von einem schweren Kreisel. Wir betrachten einen Kreisel unter dem Einfluß einer äußeren Kraft F, die am Aufpunkt A angreift. Handelt es sich um die Schwerkraft, so ist der Punkt A identisch mit dem Schwerpunkt des Kreisels. Der Kreisel rotiere um seine Symmetrieachse mit der Frequenz w. Ist das Trägheitsmoment bei Rotation um diese Achse I_z’=I_S, so ist der Drehimpuls

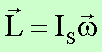
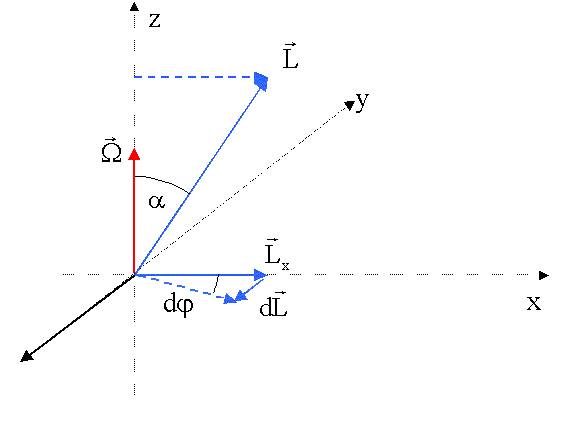
Die Kraft F erzeugt ein Drehmoment D, welches senkrecht auf L steht (in obiger Zeichnung senkrecht auf der Zeichenebene). Dieses Drehmoment erzeugt eine Drehimpulsänderung dL_y senkrecht zu L:

Unter dem Einfluss der Drehimpulsänderung dL erfolgt eine zusätzliche Rotation des Kreisels um die z-Achse mit der Winkelgeschwindigkeit W. Diese Bewegung nennt man Präzession. Mit

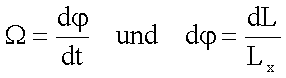
erhält man

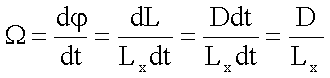
bzw.

Damit folgt allgemein

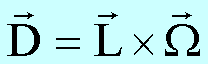
Wir diskutieren die Beziehung zwischen Drehimpuls, Drehmoment und Präzessionsfrequenz am Beispiel der Präzessionsbewegung eines Rades:

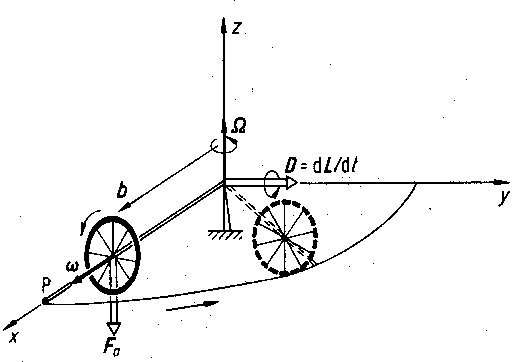
Das mit der Frequenz w um seine Symmetrieachse rotierende Rad ist auf der Achse außerhalb seines Schwerpunktes unterstützt. Das durch das Eigengewicht mg erzeugte Drehmoment

führt zu einer Präzession mit der Frequenz W um die z-Achse. Wegen

sowie und folgt für den Betrag von W: