Das Lenard-Jones-Potential

Das Lenard-Jones-Potential (LJP) beschreibt die Wechselwirkungsenergie zweier Massenpunkte im Abstand x. Die potentielle Energie kann hergeleitet werden aus der Überlagerung zweier Kräfte – einem attraktiven und einem repulsiven Anteil. An der Stelle, wo sich beide Kräfte kompensieren, hat die potentielle Energie ein Minimum:

Allgemein wird das LJP durch folgende Beziehung angegeben:

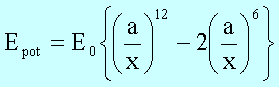
Dem Potential entspricht eine Kraft zwischen den Massenpunkten (z.B. Kraft zwischen zwei Molekülen) von

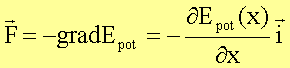
wobei den Einheitsvektor in Richtung der Kraftwirkungslinie bezeichnet, hier die x-Richtung. Man erhält durch Differenzieren

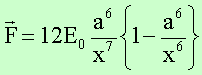
In der Gleichgewichtslage x = a ist die Kraftwirkung gleich Null.

Der Verlauf des Potentials ist in der folgenden Abbildung für a = 0,5nm und E₀ = 1eV grafisch dargestellt:

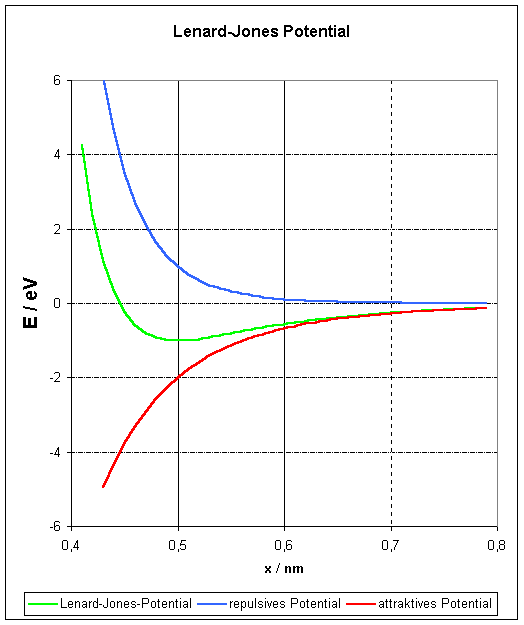
Das Gesamtpotential (grüne Kurve) hat in der Gleichgewichtslage x = a ein Minimum bei E_pot = -1 eV. Der negative attraktive Teil des Potentials nimmt mit der sechsten Potenz des abnehmenden Abstandes zu (van-der-Waals Potential). Die abstoßenden Kräfte nehmen mit abnehmendem Abstand x stärker zu, als die anziehenden, so dass ein Minimum der Energie existiert, bei dem beide Kräfte gleich stark sind.

Für x < a stoßen sich die Teilchen (Moleküle) ab und

für x > a ziehen sie sich an.

Dies hat zur Folge, dass der Gleichgewichtsabstand x » a eingenommen wird. Da die Teilchen kinetische Energie besitzen, führen sie Schwingungen um ihre Ruhelage aus. Wir untersuchen das Potential für kleine Abweichungen des Abstandes x von der Ruhelage a:

Man kann eine Funktion f(x) in der Nähe eines Punktes x = a in eine Taylorreihe entwickeln:

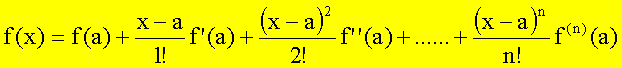
Für das LJP erhält man dann

Der ersten Ableitung der potentiellen Energie nach dem Ort entspricht die Kraft, welche an der Gleichgewichtslage den Betrag Null hat:

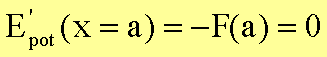
Mit Hilfe der zweiten Ableitung der potentiellen Energie nach dem Ort

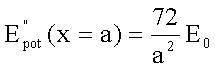
erhält man in quadratischer (harmonischer Näherung für das Potential:

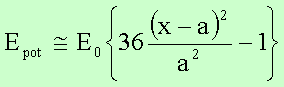
In der folgenden Abbildung ist das Potential, die quadratische Näherung sowie die Kraft in Abhängigkeit vom Abstand der Teilchen grafisch dargestellt:

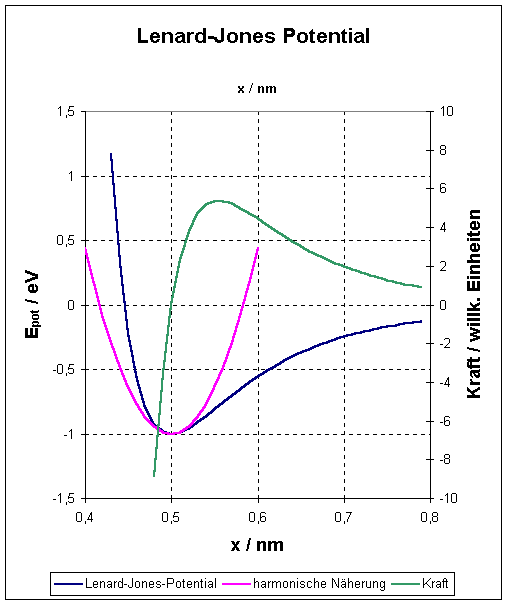
Die Minimalenergie –E₀ entspricht dem Energiebetrag, den man aufwenden muss, um die Bindung des Teilchenpaares aufzubrechen. Diese Grundzustandsenergie heißt auch Bindungsenergie oder Ionisierungsenergie. Die Kraft im Punkt x = a ist Null. Für geringere Abstände wirken abstoßende, für höhere Beträge von a anziehende Kräfte.

Die Ursache der Kräfte wurde hier nicht behandelt. Dies ist Gegenstand der Quantenmechanik. Auch die Grundzustandsenergie ergibt (bei gleichem Potential) einen anderen (höheren) von der Minimalenergie abweichenden Betrag.