Zur Newton’schen Bewegungsgleichung
Im (statischen wie dynamischen) Gleichgewicht gilt:
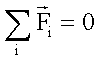
Spezialfall
zweier Kräfte:
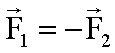
Im statischen Fall besteht z.B. Gleichgewicht zwischen dem Gewicht eines Körpers G = mg (Aktionskraft) und der elastischen Gegenkraft der Unterlage (Reaktionskraft).
Im dynamischen Fall steht die Aktionskraft (z.B. beschleunigende
Gravitationskraft) im Gleichgewicht mit der
Reaktionskraft
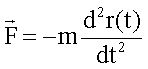
Man
kann die Kraft F als Trägheitskraft auffassen, die ein Körper einer Änderung
seines Bewegungszustandes entgegensetzt.
Beispiel Federschwinger
Die
Trägheitskraft steht im Gleichgewicht mit
a)
der Gewichtskraft mg
b)
der rücktreibenden elastischen Federkraft -Dx
Im
eindimensionalen Fall ![]() erhalten wir
erhalten wir
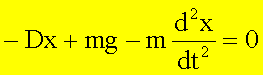
Wir
versuchen diese Bewegungsgleichung (eine Differentialgleichung zweiter Ordnung
)zu lösen. Gesucht ist der Zusammenhang x(t).
I - Eine spezielle Lösung
(statischer Fall)
Im
statischen Fall ist v = 0. Damit vereinfacht sich die Beziehung zu:
0 = -Dx + mg
Wir
erhalten daraus die spezielle Lösung x = x1:
x1 = mg/D
Diese
Lösung gibt die Ausdehnung der Feder für eine Belastung mit einem bestimmten
Gewicht an. Die Dehnung hängt von der Schwerebeschleunigung g ab.
II - Eine Lösung für den
dynamischen Fall
Wir
lösen die (homogene) Differentialgleichung für den Fall g = 0, d.h. weitab von
irgendeinem Schwerefeld:
m [ d2x(t)/dt2
] = -Dx
Mit
dem Lösungsansatz
x = xo
= xAsin(wt)
erhält
man nach dem Einsetzen in die Ausgangsgleichung:
-mw2xAsinwt + DxAsinwt = 0
Nachdem die letzte Gleichung vereinfacht und nach w umgestellt ist:
w2 = D/m
Die
Lösung lautet somit
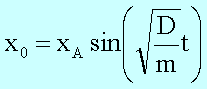
Die
letzte Gleichung beschreibt eine schwingende Feder mit der Amplitude xA
und der Frequenz
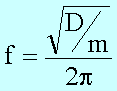
Die Feder schwingt also auch abseits von Schwerefeldern aufgrund der Wirkung der rücktreibenden Kraft –Dx.
III - Allgemeine Lösung
Die
Theorie der linearen Differentialgleichungen sagt aus, dass sich die allgemeine
Lösung aus der Summe der Lösung der homogenen Gleichung und einer speziellen
Lösung ergibt, also:
x(t) =
xo + x1
Damit
haben wir
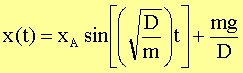
Die
Gültigkeit dieser Lösung kann leicht durch Einsetzen in die Differentialgleichung
verifiziert werden.
Die
Feder schwingt also um die (statische) Ruhelage x1 = mg/D mit der
Kreisfrequenz w2 = D/m und der Amplitude xA.
Die
Amplitude xA ergibt sich aus der in der Feder gespeicherten Energie
(hierzu später mehr).