Das Mathematische Pendel

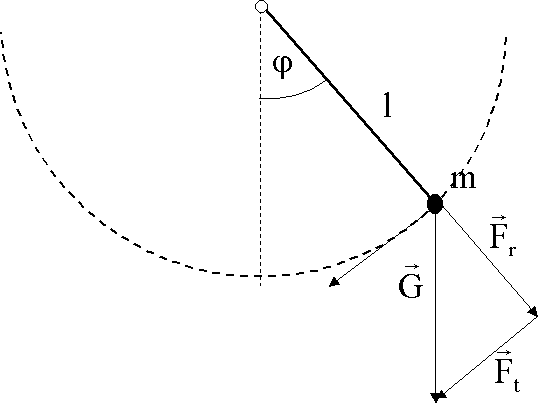
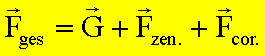
Tangentialkomponente

Die Anwendung der Newton’schen Bewegungsgleichung liefert

Die Tangentialbeschleunigung 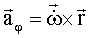hängt mit der Winkelbeschleunigung über den Kreisradius l (Pendellänge) zusammen:

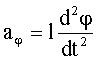
Damit erhalten wir eine homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten für die gesuchte Funktion j(t):

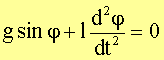
Die Sinusfunktion kann in eine Taylorreihe entwickelt werden:

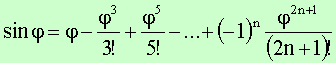
Für kleine Winkel j < 5° ist es meistens mit hinreichender Genauigkeit möglich, die Reihenentwicklung nach dem ersten Glied abzubrechen und den sinj durch j zu ersetzen, so dass gilt:

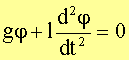bzw.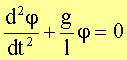

Dies ist die bekannte Schwingungsgleichung für ein mathematisches Pendel. Wir lösen diese Gleichung mit dem Ansatz

Durch Einsetzen in die Differentialgleichung erhalten wir

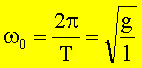
bzw. die Schwingungsdauer

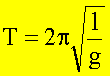
Für 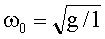ist der Lösungsansatz 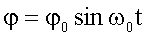eine Lösung der Schwingungsgleichung 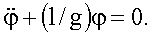In der allgemeinen Form

ist diese Differentialgleichung auf verschiedene Vorgänge anwendbar, denen eine ungedämpfte, freie Schwingung entspricht.

In Anwendung auf das mathematische Pendel hat die Tangentialkraft die bekannte Pendelbewegung mit der Schwingungsdauer zur Folge.

Diskussion der Schwingungsamplitude

Mit erhält man für die Winkelgeschwindigkeit des Pendels

Wegen (Eulergleichung) erhält man für die Tangentialgeschwindigkeit

Im tiefsten Punkt hat das Pendel die maximale Geschwindigkeit

Andererseits gilt wegen der Erhaltung der mechanischen Energie

mit

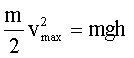
auch

Durch Vergleich beider Beziehungen folgt also für die maximale Auslenkung

wenn h die Höhe ist, auf die das Pendel zu Beginn des Schwingungsvorganges angehoben wurde.

Radialkomponente

Die Radialkomponente bestimmt die Belastung der Pendelaufhängung. Mit

setzt sich die Radialkraft aus einer Schwerkraftkomponente und einer Fliehkraftkomponente zusammen. Beschränkt man sich auf kleine Winkel (cosj » 1) erhält man mit eine Radialkraft

Drehung der Pendelebene (Foucault – Pendel)

Aufgrund seiner Trägheit behält ein Pendel die Lage seiner Schwingungsebene bezüglich eines Inertialsystems (Fixsternhimmel) bei, während die Erde rotiert. Dies führt zu einer Drehung der Pendelebene bezüglich der Erdoberfläche. Am Nordpol dreht sich die Pendelebene genau einmal pro Tag bezüglich der Erdoberfläche. An einem beliebigen Breitengrad muss man den Vektor der Winkelgeschwindigkeit der Erde zerlegen:

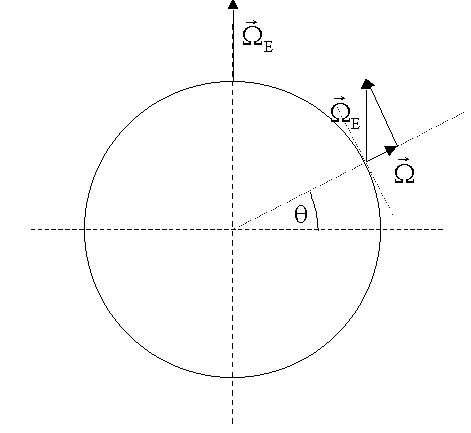
Nordpol
Äquator
Südpol