Arbeit, Potential und potentielle Energie

Als Arbeit bezeichnet man das bestimmte Wegintegral der Kraft:

Sind Kraft und Weg als Komponenten gegeben, so kann das Skalarprodukt auch folgendermaßen ausgedrückt werden:

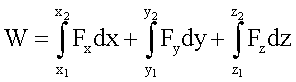
Als Potential V(x,y,z) der Kraft bezeichnet man das unbestimmte Integral (häufig wird das Potential auch als der negative Betrag des Wegintegrales der Kraft definiert und damit mit der potentiellen Energie gleichgesetzt):

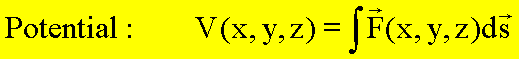
Mit Hilfe des Potentials kann man die Arbeit als Potentialdifferenz ausdrücken:

(Über den Zusammenhang zwischen Feldbegriff und Potentialbegriff siehe später). Ein Kraftfeld besitzt ein eindeutiges Potential, wenn die Arbeit zur Verschiebung einer Masse zwischen zwei Punkten und unabhängig vom gewählten Weg ist.

Dies bedeutet, dass

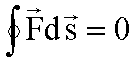
gilt. Wenn das Potential eines Feldes nur vom Ort abhängt, so ist die auf einem geschlossenen Weg verrichtete Arbeit Null. In diesem Fall kann das Kraftfeld auch eindeutig aus dem Potential abgeleitet werden und es gilt:

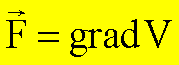
Neben dem Begriff des Potentials existiert der Begriff der potentiellen Energie. Das Potential V ist bis auf eine Konstante V₀ bestimmt. Dies hat auf den Betrag einer Potentialdifferenz (Arbeit) keinen Einfluss. Um Rechnungen praktisch zu vereinfachen, definiert man den Ort, für den das Potential gleich Null ist. Die potentielle Energie ist dann die Potentialdifferenz zu diesem Punkt, also die Arbeit, die man aufwenden muss, um einen Körper von dem Ort zum Ort mit V = 0 zu transportieren. So kann man z.B. die potentielle Energie des Gravitationsfeldes bezüglich der Meeresspiegelhöhe angeben. Zur Beschreibung der Planetenbewegung ist es günstiger, das Potential im Unendlichen gleich Null zu setzen.

, letztendlich also

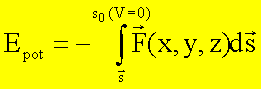bzw.

Am Beispiel des Newton’schen Gravitationsfeldes sollen diese Begriffe näher erläutert werden:

Auf eine Masse m wird im Gravitationsfeld einer Masse M folgende Kraft ausgeübt:

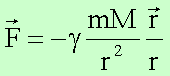
Das Potential ergibt sich dementsprechend zu

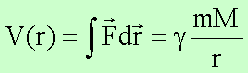
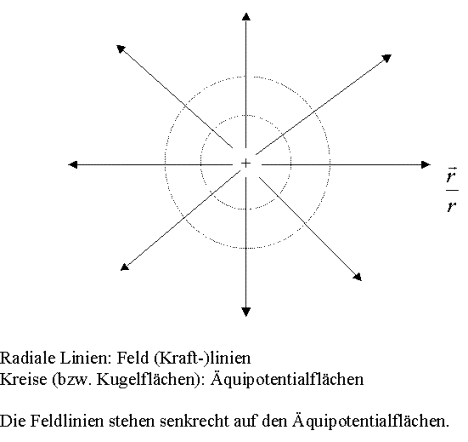
Da die Kraft nur vom Abstand r abhängt, handelt es sich um eine Zentralkraft. Linien konstanten Potentials – die sogenannten Äquipotentiallinien – sind in diesem Fall Kreise.

Um einen Körper der Masse m vom Erdboden (r = R) auf die Höhe h anzuheben, ist die Arbeit

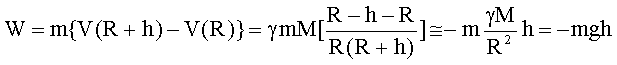
Die potentielle Energie erhält man, wenn man einen Körper vom Ort mit dem Potential V₀ = 0 auf den gewünschten Ort verschiebt.

Setzt man V₀ = V( R ) = 0 , so erhält man für die potentielle Energie

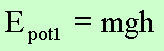
(R ist der Erdradius – Entfernung Massenschwerpunkt zu Meeresspiegelhöhe). Da der Meeresspiegel eine natürliche Äquipotentialfläche darstellt, ist dies ein guter Bezugspunkt zur Handhabung erdgebundener Probleme.

Falls V(rÞ¥) = 0 gilt, so erhält man für die potentielle Energie

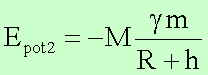
Die potentielle Energie ist in diesem Fall negativ. Diese Energieeichung wird z.B. angewandt, um die Planetenbewegung zu beschreiben. Eine wichtige Anwendung findet man auch in der Elektrostatik im Zusammenhang mit dem Coulombpotential.