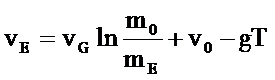Die Raketengleichung

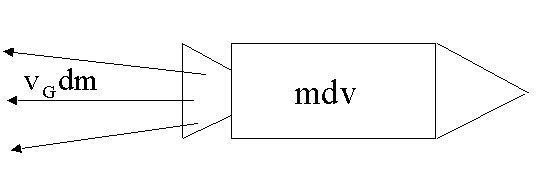
Wir begeben uns in das Schwerpunktsystem der Rakete. Im Schwerpunktsystem ist der Gesamtimpuls gleich Null und damit auch jede Gesamtimpulsänderung:

Verlässt eine Gasmasse dm die Rakete mit der Geschwindigkeit –v_G, so ändert sich der Impuls der Rakete um den Betrag mdv. Alle Geschwindigkeiten gelten bezüglich der Lage des Schwerpunktes der Rakete (zum Startzeitpunkt), der unverändert bleibt. Mit

erhält man nach Trennung der Variablen

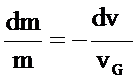
Nach der Integration

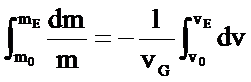
erhält man durch Einsetzen der Grenzen:

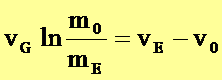
Für einen Raketenwagen (horizontale Bewegung) kann hieraus die Endgeschwindigkeit aus dem Massenverhältnis m₀ (Ausgangsmasse zu m_E (Endmasse) berechnet werden, wenn die Anfangsgeschwindigkeit v₀ und die Ausströmgeschwindigkeit der Gase bekannt sind.

Bei vertikalem Start im Schwerefeld der Erde muss noch der freie Fall im Schwerefeld berücksichtigt werden. Ist T die Flugzeit bei konstantem g (geringe Flughöhe), so erhält man für v_E: