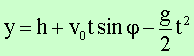Der schräge Wurf

Wir setzen im folgenden voraus, dass ein Körper unter dem Winkel j zur Horizontalen mit der Geschwindigkeit v₀ aus der Anfangshöhe h geworfen wird. Es sollen keine Reibungseffekte berücksichtigt werden. Außer der Gravitationskraft sollen keine weiteren Kräfte auf den Körper einwirken (etwa Windkraft o.ä.). In diesem Fall kann das Problem zweidimensional behandelt werden, indem wir die Bewegung in der x-y-Ebene stattfinden lassen. Die horizontale Richtung sei (d.h. entspricht der x-Achse), die vertikale Richtung (y-Achse). Damit lauten die Anfangsbedingungen folgendermaßen:

Der Körper befindet sich unter der Einwirkung der vertikalen Gravitationskraft. Die Beschleunigung sei räumlich und zeitlich konstant:

Allgemein erhält man die Geschwindigkeit mittels der Relation

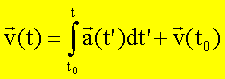
Die Vektorgleichung zerlegt man in Komponenten und integriert die Gleichung für die x- und y-Komponente getrennt. Man erhält:

Die Abhängigkeit des Ortes von der Zeit ergibt sich durch Integration von

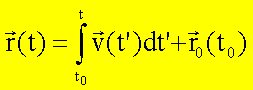
Dies führt auf folgende Komponentendarstellung für den Ort:

banane.htm

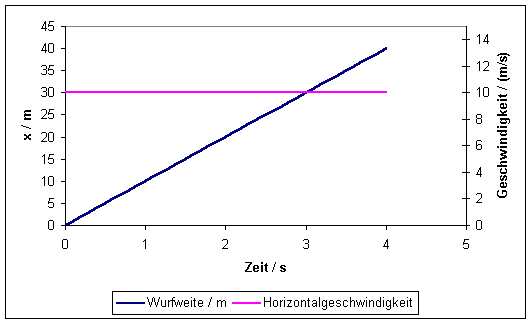
In den folgenden beiden Abbildungen sind die Funktionen x(t) und v_x(t) sowie y(t) zusammen mit v_y(t) grafisch dargestellt. Die Kurven wurden für eine Abwurfhöhe von 2m, eine Anfangsgeschwindigkeit von 20m/s und einen Abwurfwinkel von 60° berechnet (x₀ = 0). Es könnte sich um die Flugbahn eines Sektkorkens handeln.

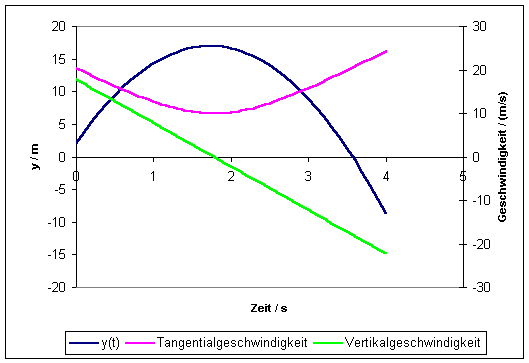
In der zweiten Grafik ist noch der Betrag der resultierenden

Tangentialgeschwindigkeit---- aufgetragen.

Aus den beiden Grafiken geht hervor, dass sich der geworfene Körper in horizontaler Richtung geradlinig gleichförmig und in vertikaler Richtung gleichmäßig beschleunigt bewegt. Das Bahnmaximum wird unter der Bedingung v_y = 0 erreicht. Aus dieser Bedingung ergibt sich für die Flugzeit bis zum Erreichen des Maximum

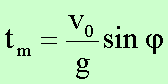
Durch Einsetzen in die Beziehung y(t_m) = y_max erhält man die maximale Flughöhe zu

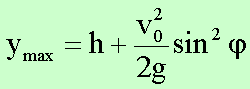
Für das angeführte Beispiel sind das t_m = Ö3 s und y_max = 17 m (vergleiche Grafik). Die Tangentialgeschwindigkeit im Scheitelpunkt muss gleich der Horizontalgeschwindigkeit von v_max = v_x = 10 m/s sein.

Die Flugbahn (Trajektorie) ist der Zusammenhang y(x). Man erhält ihn aus den Gleichungen für y(t) und x(t), indem man t eliminiert. In der folgenden Grafik ist die Flugparabel y(x) sowie die Tangential- und Vertikalgeschwindigkeit als Funktion von x dargestellt:

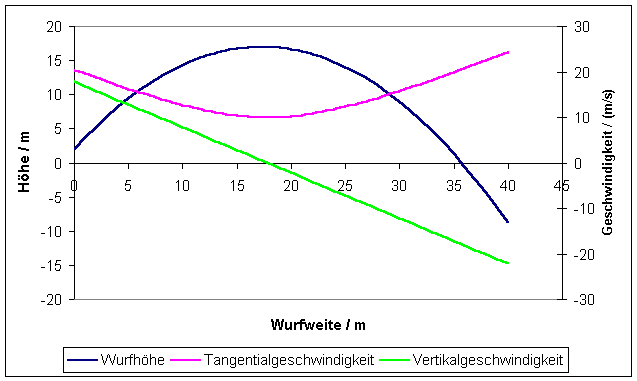
Die Bahngleichung lautet für x₀ = 0:

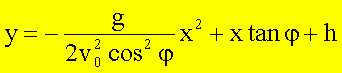
Mittels dieser Gleichung kann die Wurfweite aus der Bedingung y = 0 berechnet werden. Man erhält

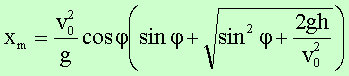
Im oberen Beispiel erhält man eine Flugweite von etwa 36m. Mittels der letzten Gleichung kann man die Frage beantworten, unter welchem Winkel man einen Körper abwerfen muss, damit die Flugweite maximal wird. Dazu muss die Extremwertaufgabe

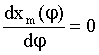gelöst werden. Für den vereinfachten Fall h = 0 erhält man aus der Gleichung sinj = cosj den Winkel j_max = 45°. In der folgenden Grafik ist die Reichweite (y = 0) für unser Beispiel aufgetragen:

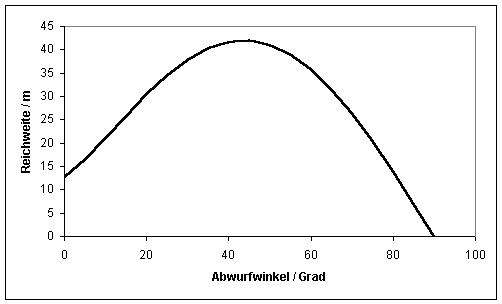
Für 45° erhält man x_m = 41,9 m, für 60° x_m = 35,8m. Im Falle eines waagerechten Wurfes fliegt der Körper lediglich 12,6m.