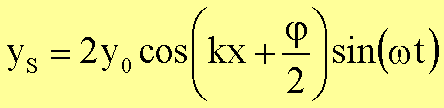Stehende Wellen

Wir betrachten die Amplitude einer harmonischen Welle y₀, etwa einer Wasser- oder Seilwelle y(x,t) = y₀sin(wt + kx). Die Amplitude verschiebt sich mit der Phasengeschwindigkeit c = w/k entlang der Ausbreitungsrichtung. Im Falle der Reflexion der Welle an einem Hindernis, etwa einer Wand, überlagert sich die einlaufende Welle mit der rücklaufenden Welle y_R(x,t) = y₀sin(wt - kx). Da die rücklaufende Welle die entgegengesetzte Ausbreitungsrichtung hat, ist hier k durch –k ersetzt. Für die Superposition beider Wellen erhält man aus

mit Hilfe des Additionstheorems

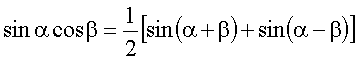
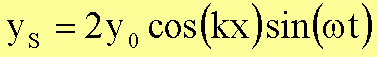
Wir erhalten einen Ausdruck, der eine Welle beschreibt, deren Amplitude im Raum zu stehen scheint, deren Amplitudenbetrag aber entsprechend einer Kosinusfunktion im Raum verläuft. Es gibt Stellen im Abstand l/2, an denen die Amplitude immer Null ist, die sogenannten Knoten, sowie Punkte, an denen die Amplitude ein relatives Maximum hat, die sogenannten Bäuche. Die Welle schwingt zeitlich periodisch auf und ab entsprechend dem räumlichen Verlauf der Amplitude.

Der Wechsel von k auf –k bei der Reflexion entspricht einem Phasensprung von 180°. Dies bedeutet, dass an der reflektierenden Wand die Auslenkung von y auf –y wechselt, woraus wiederum folgt, dass die Überlagerung aus ein- und auslaufender Welle an der Wand die resultierende Auslenkung y_S(x = x_Wand) = 0 ergibt. Dies ist in der Regel auch die Randbedingung bei einer „harten“ Reflexion.

(Beispiel: Seilwelle – ist das Seil an einer Wand befestigt, ist die Auslenkung aufgrund der experimentellen Bedingungen gleich Null).

Die Überlagerung einer reflektierten Welle mit der einlaufenden Welle ist in den folgenden Grafiken dargestellt:

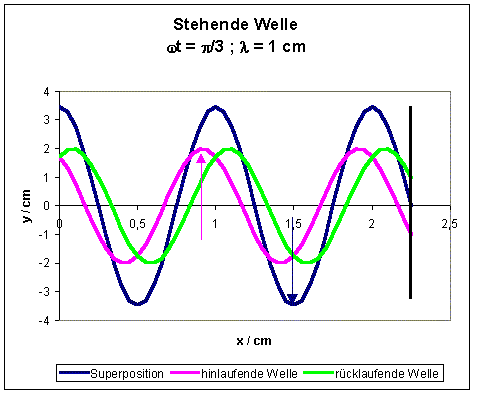
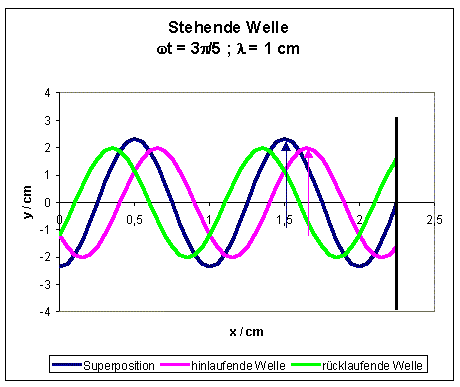
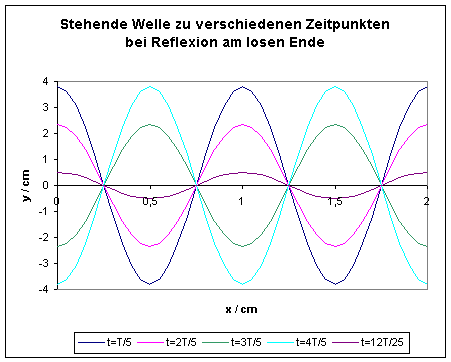
In der folgenden Abbildung ist noch einmal die Auslenkung y_S(x) der stehenden Welle zu verschiedenen Zeitpunkten aufgetragen:

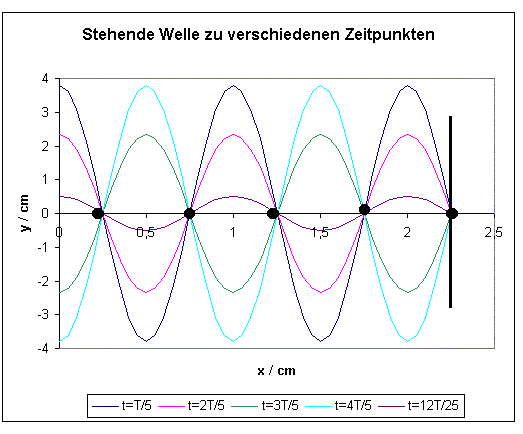
: Knoten ; dicke Linie: reflektierende Wand

Die Abbildung verdeutlicht, dass sich die Position der Knoten und Bäuche mit der Zeit nicht ändert – die Welle “steht“ im Raum. An der reflektierenden Wand befindet sich ein Knoten. Ist die Auslenkung an der Wand durch die experimentellen Bedingungen nicht hart auf Null gesetzt (weiche Reflexion, wie z.B. an einem locker befestigten Seil), so findet kein Phasensprung statt.

In allgemeinen Fall einer Überlagerung von hin- und rücklaufenden Wellen, zwischen denen eine Phasenverschiebung j besteht

enthält die Phase den zusätzlichen Phasenwinkel j/2. Man erhält nunmehr folgendes Ergebnis:

Wir ersetzen nunmehr noch x durch die Koordinate x’ = x-x₀, wobei x₀ die Koordinate der Wand bezeichnet, an der der Phasensprung stattfindet. Die Auslenkung der stehenden Welle bezieht sich dann auf den Abstand zur Wand:

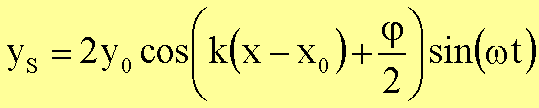
Bei Reflexion am festen Ende ist j = p und y_S(x=x₀) = 0. An der Wand befindet sich ein Schwingungsknoten.

Bei Reflexion am losen Ende ist j = 0 und y_S(x=x₀)= 2y₀sin(wt). An der Wand befindet sich ein Schwingungsbauch.

Die folgende Abbildung stellt eine stehende Welle dar, bei der sich die Wand an der Stelle x = x₀ = 2cm befindet: