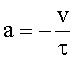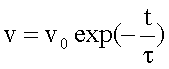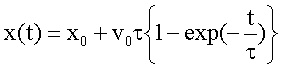Geschwindigkeitsabhängige Beschleunigung

( Beispiel Stokes'sche Reibung)

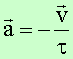
Anfangsbedingungen:

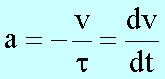
Trennung der Variablen v und t ermöglicht Integration:

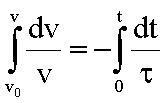
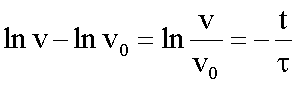
Aus der Abhängigkeit v(t) folgt durch nochmalige Integration das Weg- Zeit-Gesetz:

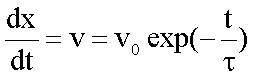
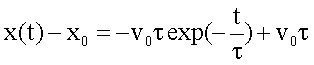
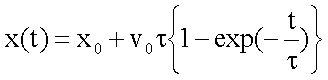
t	a	v	x
0
¥	0	0
t’

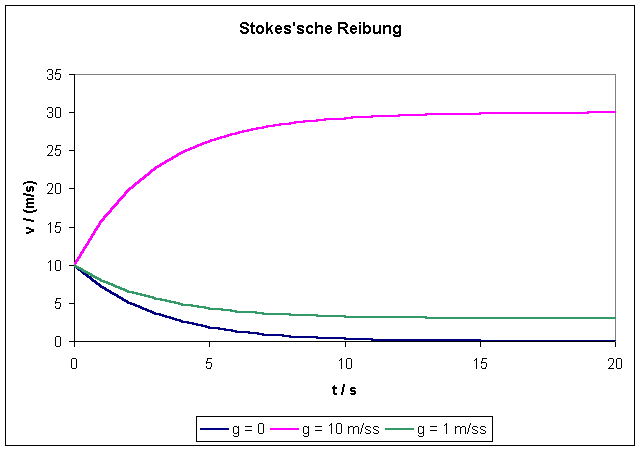
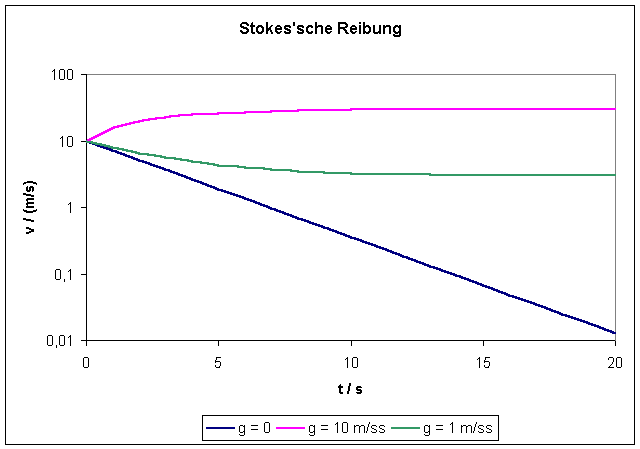
Wirkt zusätzlich eine zeitlich konstante Beschleunigung in derselben Richtung, also etwa

wie z.B. beim freien Fall einer Kugel in einer Flüssigkeit (hier wäre dann allerdings noch die Auftriebskraft zu berücksichtigen), so geht man folgendermaßen vor: Die Bewegungsgleichung

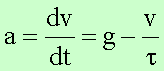
hat die spezielle Lösung

Diese Lösung entspricht der Bewegung des Körpers für Zeiten t>>t.

Die allgemeine Lösung der Bewegungsgleichung erhält man als Summe (Linearkombination) beider Lösungen unter Berücksichtigung der Anfangsbedingungen (siehe später Mathematikvorlesung zum Thema lineare Differentialgleichungen):

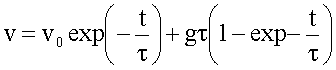
Integration dieser Beziehung liefert die Weg-Zeit-Relation. Der Körper bewegt sich mit der Anfangsgeschwindigkeit v₀ und bewegt sich für t >> t mit der konstanten Geschwindigkeit gt.