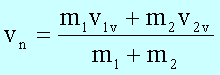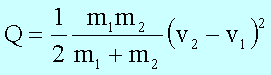Stöße zwischen Teilchen

Wir betrachten den Stoß zweier Körper mit den Massen m₁ und m₂. Bei einem Stoß, einer kurzzeitigen Wechselwirkung, wirken nur innere Kräfte, so dass der Gesamtimpuls aller Teilchen erhalten bleibt:

Während des Stoßes bleibt die mechanische Energie nur in speziellen Fällen erhalten, da ein Teil der Energie während des Stoßes in andere Energieformen, wie Wärme oder Deformationsenergie umgewandelt wird. Es gilt jedoch der Satz von der Erhaltung der Gesamtenergie:

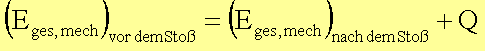
Mechanische Energie ist hier im allgemeinen kinetische Energie und unter Q ist eine nichtmechanische Energieform, z.B. Wärme, zu verstehen. E_{ges, mech} beinhaltet die gesamte mechanische Energie aller am Stoß beteiligten Teilchen. In Abhängigkeit vom Betrag der Größe Q unterscheidet man folgende Fälle:

	Bezeichnung	Beispiel
	elastischer Stoß	Kugelstoß
	inelastischer Stoß	ballistisches Pendel
	superelastischer Stoß	Kernfusion

Der zentrale, elastische Stoß zweier Körper

Bei einem zentralen Stoß sind die Impulsvektoren aller am Stoß beteiligten Körper vor und nach dem Stoß parallel zueinander. Das Problem kann eindimensional behandelt werden, so dass sich die aus dem Impulserhaltungssatz folgenden drei Gleichungen auf eine reduzieren. Es gelten mit dem Energie- und Impulserhaltungssatz folgende Beziehungen:

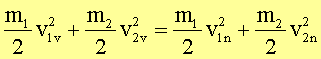
Die Indizes v und n bedeuten vor dem Stoß und nach dem Stoß. Sind die Geschwindigkeiten vor dem Stoß bekannt, so kann man aus obigem Gleichungssystem die Geschwindigkeiten nach dem Stoß berechnen:

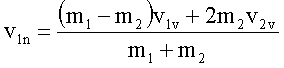
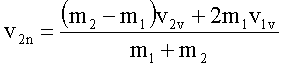
Der nichtzentrale, elastische Stoß zweier Körper

Wir behandeln den Spezialfall des nichtzentralen Stoßes zweier Kugeln gleicher Masse m, wobei eine Kugel (Nr. 2) vor dem Stoß ruht.

Mit den Erhaltungssätzen

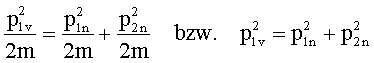
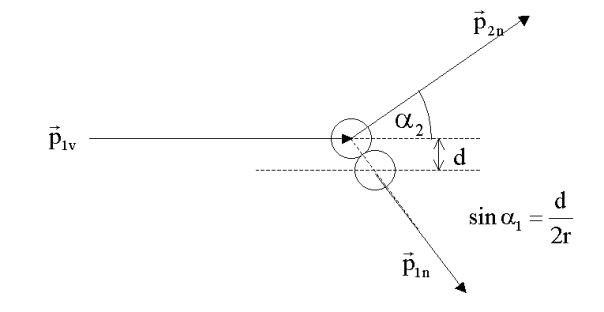
erhält man folgendes Bild:

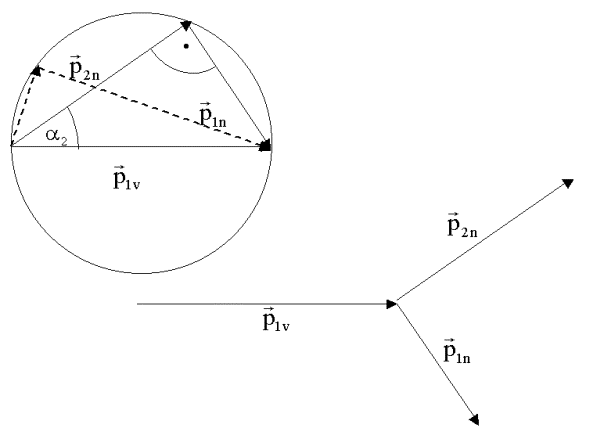
Die Summation dreier Impulse lässt sich als ebenes Problem behandeln. Damit kann man bei geeigneter Wahl des Koordinatensystems die drei Impulsgleichungen (die aus der Vektorgleichung folgen) auf zwei Gleichungen reduzieren. Des weiteren schließen die beiden Impulsvektoren p_1n und p_2n einen rechten Winkel ein. Dies ist eine Folge der gleichen Massen. Nur in diesem Fall können die Beträge der Impulse entsprechend der Energiegleichung pythagoräisch addiert werden. Damit lassen sich die Geschwindigkeiten der Kugeln nach dem Stoß sofort ermitteln, wenn der Winkel a₂ (bzw. a₁) bekannt ist (hängt von den Bedingungen beim Stoß ab):

Außerdem gilt

mit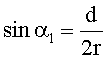

Der Winkel a₁ ergibt sich aus der Neigung der Verbindungslinie der Schwerpunkte beider Kugeln zur Impulsrichtung p_1v.

stoss\stoss.html




Der vollkommen unelastische Stoß

Die Gültigkeit des Impulserhaltungssatzes setzt nicht voraus, dass der Satz von der Erhaltung der mechanischen Energie gilt. Auch für den Fall Q ¹ 0 gilt deshalb für den St0ß zweier Körper:

Die allgemeine Energieerhaltung bedingt:

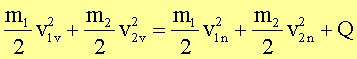
Ein Spezialfall des unelastischen Stoßes liegt vor, wenn sich die beiden Körper nach dem Stoß gemeinsam (mit gleicher Geschwindigkeit v_n) fortbewegen. In diesem Fall ist der maximal mögliche Teil von kinetischer Energie in Deformationsenergie umgewandelt worden. Hätten sich die Körper wenigstens zum Teil elastisch deformiert, wäre ein Teil der mechanischen Deformation wieder in kinetische Energie zurückgeführt worden, was ungleiche Geschwindigkeiten der beteiligten Körper zur Folge gehabt hätte. Es gilt in diesem speziellen Fall also:

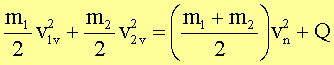
Gilt weiterhin , so erhält man folgende Beziehungen :

stoss.htm