Das Thomson’sche Atommodell

Modellvorstellung:

Ein Elektron schwingt innerhalb einer homogen positiv geladenen Kugel vom Radius R.

Es sei r der Abstand zum Mittelpunkt der Kugel. Der Betrag des elektrischen Feldes einer homogen elektrisch geladenen Kugel ergibt sich mit r als Volumenladungsdichte zu

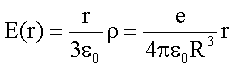
Die Bewegungsgleichung einer Ladung e der Masse m im Kraftfeld der geladenen Kugel lautet:

bzw.

Dies ist die Gleichung einer harmonischen, ungedämpften Schwingung

mit der Eigenfrequenz

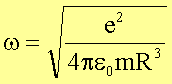
Setzt man für R den Bohr’schen Radius

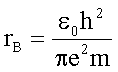
ein, so erhält man

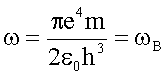
Für den Fall R = r_B stimmt also die Umlauffrequenzen des Bohr’schen Modells mit der Oszillationsfrequenz im Thomson’schen Modell überein. Diese Frequenz hat jedoch nichts mit Übergangsenergien zu tun, die man in Emissionsspektren beobachten kann.