Das Vektorprodukt
Zur geometrischen Bedeutung des Vektorproduktes:
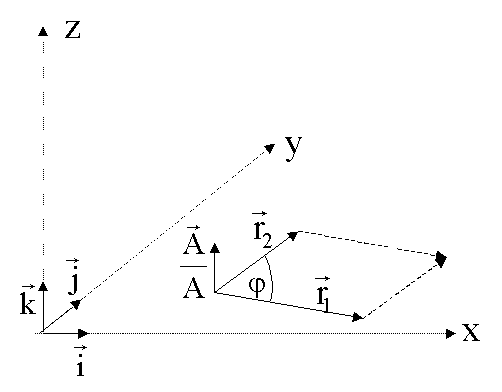
Das Vektorprodukt (Kreuzprodukt) zweier Vektoren 
und 
, die von demselben Punkt P ausgehen, ergibt einen Vektor,
·
dessen
Betrag der Fläche des von den beiden Vektoren aufgespannten Parallelogramms und
·
dessen
Richtung der Flächennormale des aufgespannten Parallelogramms entspricht.
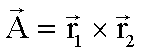
Sind zwei Vektoren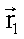 
und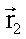 
in
Komponentenschreibweise gegeben, so wird das Vektorprodukt 
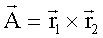folgendermaßen
berechnet (hier sind die xi und yi Koordinaten, wenn der
Ursprung des Koordinatensystems mit P zusammenfällt) :
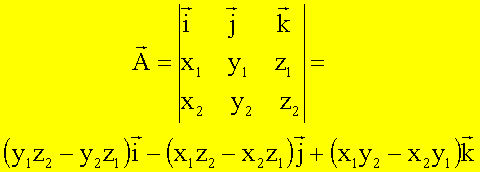
Der
Betrag des Vektorproduktes ergibt sich dann folgendermaßen:
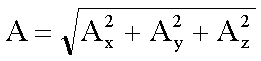
