Wellen – die Wellengleichung

Eine Welle entspricht einem physikalischen Vorgang, bei welchem sich eine Schwingung im Raum ausbreitet. Dabei wird Energie und Impuls zwischen Oszillatoren übertragen.

Eine physikalische Größe y(x,t), die die Schwingung eines Oszillators am Ort x zur Zeit t beschreibt (z.B. Schwingung eines Atoms im Kristallgitter), überträgt ihre Energie an einen benachbarten Oszillator, wodurch dieser zeitlich verzögert zu schwingen beginnt. Die Ausbreitung der Schwingung wird durch die Wellengleichung (d’Alambert-Gleichung)

beschrieben. Im eindimensionalen Fall, der uns im weiteren interessieren soll, geht über in

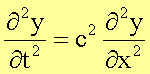
Der Größe y(x,t) soll hier eine Koordinate entsprechen, also etwa der Auslenkung eines Wassermoleküls bei der Ausbreitung einer Wasserwelle. Im allgemeinen kann es sich jedoch auch um jede einen Schwingungsvorgang beschreibende Größe handeln, wie etwa den Druck oder das elektrische Feld. Die Größe c hat die Dimension einer Geschwindigkeit und hängt mit der Ausbreitungsgeschwindigkeit der Welle – der sogenannten Phasengeschwindigkeit – zusammen.

Funktionen der Gestalt

sind Lösungen der Wellengleichung wegen und . Das Argument bezeichnet man als Phase der Welle. Hat ein Oszillator zum Zeitpunkt t = 0 am Ort x die Auslenkung y, so hat (hatte) er dieselbe Auslenkung am Ort zum Zeitpunkt . Die Phase hat sich dabei mit der Geschwindigkeit c ausgebreitet.

Transversale elastische Wellen

Wir betrachten ein gespanntes elastisches Seil, das an einer beliebigen Stelle x transversal aus seiner Ruhelage in y-Richtung ausgelenkt wird (z. B. durch einen kurzen kräftigen Schlag - siehe Hörsaalversuch):

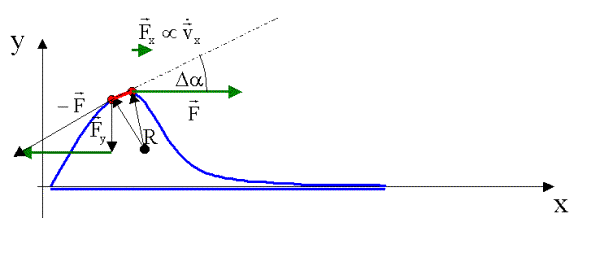
Durch die Auslenkung wird das Seil tangential gespannt, wodurch sich der Abstand zwischen zwei Seilpunkten verändert. Zerlegt man das an einem Seilstück zwischen zwei Punkten angreifende Kräftepaar in seine x- und y-Komponente, so ergibt sich (in oberer Abbildung) eine resultierende Komponente F_x, welche eine Verschiebung des Seilstückes in x-Richtung mit der Geschwindigkeit v_x verursacht. Die Komponente F_y verändert die Auslenkung in y-Richtung.

Aufgrund der Krümmung des Seiles ist das am Seilstück der Länge Dx angreifende Kräftepaar um den Winkel Da gegeneinander verdreht. Für die resultierende Kraft in y-Richtung erhält man:

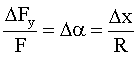
Die Größe R ist der Krümmungsradius des Seilstückes entsprechend der Definition . Die Beschleunigung in y-Richtung ergibt mittels der Seilspannung s = F/A zu

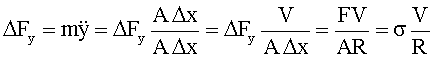
bzw.:

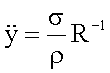
Für geringe Auslenkungen y kann der Krümmungsradius ausgedrückt werden durch die Beziehung . Damit erhalten wir unsere Wellengleichung zu

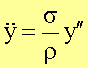
Wir suchen eine spezielle Lösung dieser Wellengleichung mit dem Ansatz

Mit

erhält man die Beziehung für die Phasengeschwindigkeit

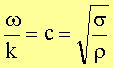
Die Lösung bezeichnet man als ebene monochromatische Welle. Ihre Eigenschaften sollen im folgenden näher diskutiert werden.