Zum allgemeinen linearen Modell siehe: Schäfer (2016).
Um das gewichtete Mittel über den Vektor
zu bestimmen, stellt man ein allgemeines lineares Modell mit nur
einem Parameter 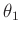
und der der
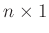 Design-Matrix
Design-Matrix
auf. Die Unsicherheiten 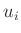 der Werte
der Werte 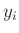 definieren die
definieren die
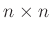 Gewichtsmatrix
Gewichtsmatrix
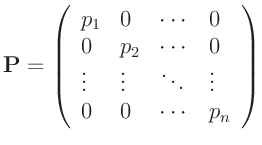 mit
mit 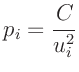
wobei C eine willkürlich festgelegte Konstante ist.
Durch Anwendung der Gleichungen 12 bis 14 aus Schäfer (2016)
folgt daraus:
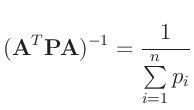 und
und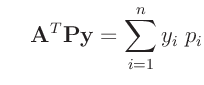
Damit ergibt sich für den Schätzwert des gewichteten Mittels
Mit dem Schätzwert für die Varianz
folgt aus dem linearen Modell für die Varianz des geschätzten Parameters 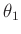 :
:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
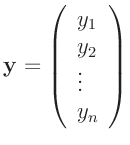
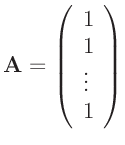
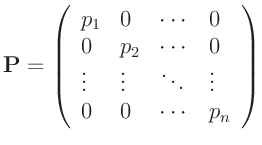 mit
mit 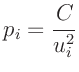
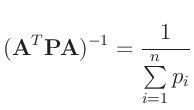 und
und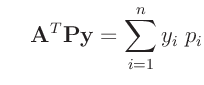
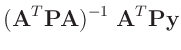
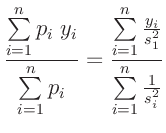
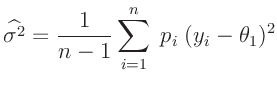
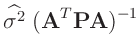
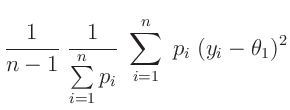
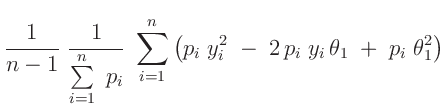
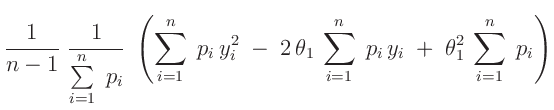
![$\displaystyle \frac{1}{n-1}\left[\frac{\sum\limits_{i=1}^n\;p_i\,y_i^2}{\sum\limits_{i=1}^n\;p_i}\;
-\;\theta_1^2\right]$](img94.png)
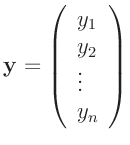
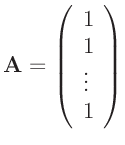
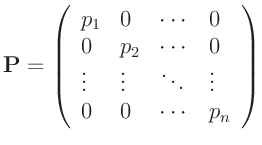 mit
mit 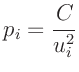
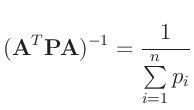 und
und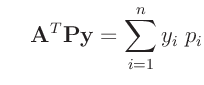
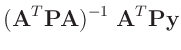
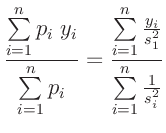
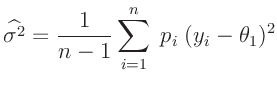
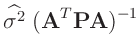
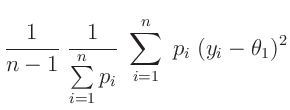
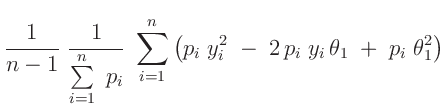
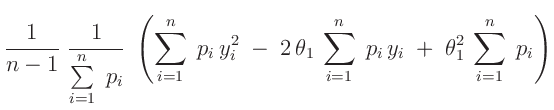
![$\displaystyle \frac{1}{n-1}\left[\frac{\sum\limits_{i=1}^n\;p_i\,y_i^2}{\sum\limits_{i=1}^n\;p_i}\;
-\;\theta_1^2\right]$](img94.png)