Auswertung Versuch F1-Fehlerverteilung mit GnuPlot

Der Versuch F1 (Einführungspraktikum (2007) Seite 1 und 2) beschäftigt sich mit einer Ursache der Messunsicherheit und deren statistischen Verteilung. Messen bedeutet Vergleichen. Eine physikalische Größe, z.b. eine Länge, wird mit Hilfe eines Messgerätes, z.b mit Hilfe eines Lineals, mit einem definierten Normal verglichen. Um diesen Vergleich für unterschiedliche Werte der zu messenden Größe zu vereinfachen, ist das Messgerät fast immer mit einer Skala ausgestattet, auf der sich der gesuchte Wert ablesen lässt, entweder direkt oder mit Hilfe eines Zeigers. Der Ablesevorgang selbst ist eine Ursache der Messunsicherheit, unabhängig davon, ob der Experimentator diesen selbst ausführt oder die Umsetzung mit elektronischen Hilfsmitteln (digitale Messgeräte) erfolgt.

Den Versuch F1 kann jeder auf seinem eigenen Computer durchführen. Dazu werden das Programm GnuPlot und das GnuPlot-Skript F1.gnuplot benötigt. Durch Eingabe des Befehls

load "F1.gnuplot"

in das Terminalfenster von GnuPlot wird der Versuch gestartet.

Abbildung 1: Versuch F1

In dem sich öffnenden Grafikfenster wird nach einem Vorspann eine Skala von 0 bis 10 mit einer Unterteilung in Schritten von 0.5 gezeigt. An einer zufällig gewählten Position dieser Skala ist ein Zeiger dargestellt (linke Seite von Abbildung 1). Die Position des Zeigers soll mit 2 Nachkommastellen geschätzt und notiert werden. Nach 5 Sekunden wird darunter der wahre Wert der Zeigerposition, auf drei Nachkommastellen gerundet, für weitere 4 Sekunden angezeigt (rechte Seite von Abbildung 1). Dieser ist ebenfalls zu notieren. Auf diese Weise entsteht eine Messwertetabelle mit 100 Wertepaaren.

Die weitere computergestützte Auswertung kann auch mit dem Programm GnuPlot erfolgen. Dazu ist als erster Schritt diese Tabelle mit einem einfachen Texteditor in eine Datei, z.B. ,,daten.txt`` zu übertragen, jedes Wertepaar in eine eigene Zeile, in der ersten Spalte der abgelesene Wert, in der zweiten Spalte der wahre Wert. Die Differenz zwischen abgelesenem Wert und wahrem Wert ist der Ablesefehler, dessen Statistik im weiteren untersucht werden soll. Gibt man in das Terminalfenster von GnuPlot den Befehl

stats "data.txt" using ($1-$2);

so erhält man eine Vielzahl von Informationen über die Verteilung des Ablesefehlers. Sollte stattdessen die Warnung ``Can't read data file'' erscheinen, ist mit dem Befehl

cd "Pfad zur Datei data.txt"

in das Verzeichnis zu wechseln, in dem die Datendatei gespeichert ist. Der aktuelle Pfad, das aktuelle Arbeitsverzeichnis, kann mit

pwd

abgefragt werden. Mit den Pfeiltasten up und down kann in der Liste der zuvor eingegebenen Befehle geblättert werden. Damit können diese erneut editiert und ausgeführt werden.

Für die weitere Auswertung werden die Größen $x_{min}$, $x_{max}$ und die Anzahl der Datenpunkte benötigt.

print STATS_min
print STATS_max
ntotal = STATS_records

Für die Darstellung des Histogramms sollten die Werte für $x_{min}$ und $x_{max}$ von Hand so festgelegt werden, dass alle Datenpunkte enthalten sind. In diesem Beispiel:

xmin = -0.26
xmax = 0.26

Für die spätere Verwendung können auch gleich die beiden Werte für den Mittelwert und die Standardabweichung übernommen werden.

mw = STATS_mean
std = STATS_stddev

Zur Darstellung der Häufigkeitsverteilung wird der Bereich $x_{min} \ldots x_{max}$ in eine geeignete Anzahl von gleich großen Intervallen unterteilt. In jedem sollte wenigstens 1 Messpunkt enthalten sein. Für die Anzahl der Intervalle gibt es unterschiedliche Empfehlungen. Im Einführungsskript (2007) wird auf Seite 23 ohne weitere Begründung $N \approx 5 \log_{10} n$ angegeben. Viele Statistiklehrbücher beziehen sich auf Sturges (1926), der für die Intervallebreite $\Delta x = r/(1 + 3.322 \log_{10} n)$ vorschlägt. $r$ ist der Bereich der Datenwerte $(x_{max}-x_{min})$. Scott (1979) nutzt die aus den Daten bestimmte Standardabweichung um die Intervallbreite festzulegen. $\Delta x = 3.5\,\widehat{\sigma}\,n^{-1/3}$. Aus der Intervallbreite und dem Bereich der Datenwerte ergibt sich dann die Intervallanzahl. Hier wird mit $N=10$ weitergerechnet.

ncolumn = 10

Als nächster Schritt ist die Häufigkeitstabelle zu erstellen. Diese enthält in der ersten Spalte den Mittelpunkt $(xmin_i + xmax_i)/2$ des jeweiligen Intervalls, in der zweiten Spalte die Anzahl der Messpunkte $n_i$ die innerhalb des Intervalls liegen. In der dritten Spalte wird gleich noch der Wert der Summenhäufigkeit, der Summe $\sum_{j=1}^i n_j$ eingetragen. Diese Tabelle, die in einer zweiten Datei z.B. ,,histogrammdata.txt`` abgespeichert wird, kann entweder per Hand oder auch mit dem Programm GnuPlot erstellt werden. Dazu ist als nächstes die Intervallbreite zu berechnen, der Dateinamen festzulegen und der Startwert für die Summenhäufigkeit auf 0 zu setzen.

xdelta = (xmax-xmin)/ncolumn
set print 'histogrammdata.txt'
shn = 0

Durch Verwendung des schon bekannten Kommandos stats lässt sich die Anzahl der in jedem Intervalle enthaltenen Messwerte abfragen. Dazu ist die Angabe der Bereichsgrenzen notwendig. Da wir nur eine Spalte von Werten, die Differenz zwischen Messwert und wahrem Wert, verarbeiten, wird diese von GnuPlot als Spalte von y-Werten betrachtet. Als x-Werte werden in diesem Fall die Zeilennummer in der Datendatei angesehen. Mit dem komplexen Befehl

do for [i = 1:ncolumn] {
xmax = xmin + xdelta
set yrange [xmin:xmax]
stats "data.txt" using ($1-$2) nooutput;
n = STATS_records
shn = shn + n
print sprintf("% .3f %3i %3i",(xmin+xmax)/2, n, shn)
xmin = xmax
}

wird die Datei mit den Histogrammdaten erzeugt. Erst nach Eingabe der letzten schließenden Klammer erfolgt die Bearbeitung. Die Fehlermeldung ,,All points out of range`` bedeutet, dass ein Intervall keine Datenpunkte enthält. In diesem Fall ist die Anzahl der Intervalle zu verringern oder die Werte von $x_{min}$ und $x_{max}$ leicht zu verändern. Als nächstes ist die Datei mit den berechneten Histogrammdaten noch mit dem Kommando

set print

zu schließen. Der letzte Wert der Summenhäufigkeit sollte mit der Anzahl der Datenpunkte übereinstimmen. Dies lässt sich leicht mit

print shn, ntotal

überprüfen. Die Festlegung der y-Bereichsgrenzen ist auf das Standardverhalten zurückzusetzen

unset yrange

und die Achsenbeschriftung festzulegen

set xlabel "Messabweichung"
set ylabel "absolute Häufigkeit"

Nun kann das Histogramm gezeichnet werden.

plot "histogrammdata.txt" using 1:2 with boxes notitle;

Die Höhe der einzelnen Balken gibt die Anzahl der Datenpunkte in den jeweiligen Intervall an. Das Verhältnis $n_i/n_{total}$ entspricht der Wahrscheinlichkeitsdichtefunktion der zu Grunde liegenden statistischen Verteilung, die sich für $n_{total}\rightarrow\infty$ und $\Delta x \rightarrow 0$ ergäbe. In sehr vielen Fällen ist dies die Dichtefunktion der Gauß-Verteilung

$$f(x) = \frac{1}{\sigma \sqrt{2\,\pi}}\; e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$$

mit dem Mittelwert $\mu$ und der Standardabweichung $\sigma$.

dg(my,sigma,x) = exp(-0.5*((x-my)/sigma)**2)/(sigma*sqrt(2*pi))

Mit den anfangs aus den Daten bestimmten Werten für den Mittelwert und die Standardabweichung kann die zu dem Histogramm Dichteverteilung gezeichnet werden.

plot "histogrammdata.txt" using 1:2 with boxes notitle, \
xdelta*ntotal*dg(mw,std,x) with lines notitle;

Wahrscheinlichkeitsdichtefunktionen sind immer normiert. Für sie gilt

$$\int_{-\infty }^{\infty } f(x) \, dx = 1$$

Das heißt, die Fläche unter der Dichtekurve hat den Wert 1. Der zusätzliche Faktor xdelta*ntotal entspricht der Fläche aller Balken des Histogramms. Damit wird die Fläche unter der gezeichneten Dichteverteiling genauso groß, wie die Fläche des Histogramms.

Abbildung 2: Histogramm mit Gauß-Verteilung

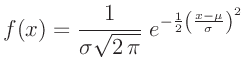
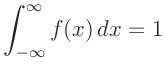
Wesentlich besser lässt sich die Übereinstimmung zwischen der Verteilung der Datenpunkte und einer gegebenen Wahrscheinlichkeitsverteilung mit Hilfe der Verteilungsfunktion beurteilen. Diese ist allgemein definiert durch:

$$F(x) = \int_{-\infty }^x f(t) \, dt$$

Für die Normalverteilung ergibt sich daraus:

$$F(x) = \frac{1}{\sigma \sqrt{2\,\pi}}\; \int_{-\infty }^x \; e^{-\frac{1}{2}\left(\frac{t-\mu}{\sigma}\right)^2}\,dt$$

Mit der Substitution $z=\frac{t-\mu}{\sigma}$ kann diese auf die Verteilungsfunktion der Standardnormalverteilung $\Phi(x)$, der Normalverteilung mit $\mu=0$ und $\sigma=1$ zurückgeführt werden.

$$F(x) = \frac{1}{\sqrt{2\,\pi}}\; \int_{-\infty }^{\frac{x-\mu}{\sigma}} \; e^{-\frac{1}{2}\,z^2}\,dz$$

$$= \Phi\left(\frac{x-\mu}{\sigma}\right)$$

Die Verteilungsfunktion der Standardnormalverteilung kann, so sie nicht als eigenständige Funktion definiert ist, auch mit Hilfe der Fehlerfunktion $\mathrm{erf}(x)$ berechnet werden.

$$\Phi(x) = \frac{1}{2}\left(1 + \mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)\right)$$ (1)

In GnuPlot kann die Verteilungsfunktion der Standardnormalverteilung mittels der Funktion norm(x) berechnet werden. Damit lassen sich die berechneten Summenhäufigkeiten zusammen mit der erwarteten Verteilungsfunktion zeichnen.

set yrange [0:105]
set ylabel "absolute Summenhäufigkeit"
plot "histogrammdata.txt" using 1:3 notitle,\
ntotal*norm((x-mw)/std) with lines notitle;

Abbildung 3: Summenhäufigkeit mit Verteilungsfunktion der Gauß-Verteilung

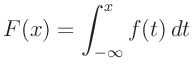
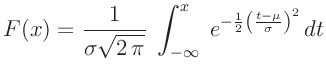
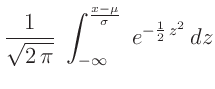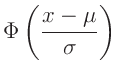Die Abweichungen sind bei dieser Darstellung (Abbildung 3) besser zu erkennen. Noch deutlicher könnten diese werden, wenn die y-Achse des Graphen in einer solchen Weise geteilt wäre, dass die Verteilungsfunktion eine Gerade ergäbe. Dies ist durch eine Skalierung mit der Umkehrfunktion der Verteilungsfunktion (Gleichung 1) zu erreichen.

$$x(\Phi) = \sqrt{2}\,\mathrm{erf}^{-1}\left(2 \Phi - 1\right)$$ (2)

Darin ist $\mathrm{erf}^{-1}$ die inverse Fehlerfunktion, die Umkehrfunktion der Fehlerfunktion. Durch die Anwendung dieser Funktion, die in GnuPlot als invnorm(x) bereits definiert ist, auf die y-Werte des Graphen, wird die Verteilungsfunktion als Gerade

$$y = \frac{1}{\sigma}\left(x\,-\,\mu\right)$$

dargestellt.

unset yrange
set ylabel "sigma"
plot "histogrammdata.txt" using 1:(invnorm($3/ntotal)) notitle,\
((x-mw)/std) with lines notitle;

Abbildung 4: Skalierte Darstellung der Summenhäufigkeit und der Verteilungsfunktion der Gauß-Verteilung

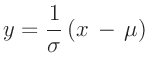
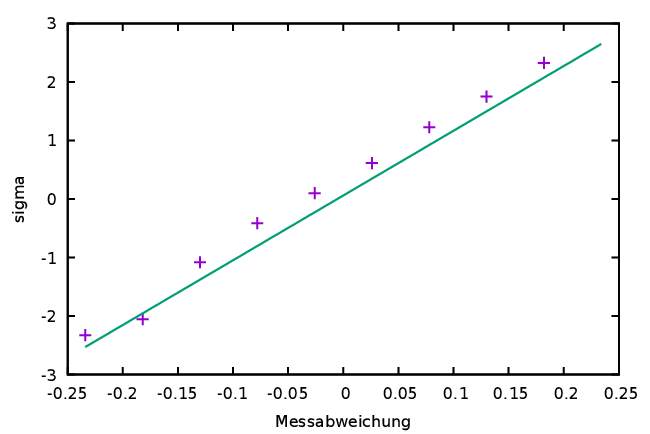Bei dieser Darstellung (Abbildung 4) ist die y-Achse in Vielfachen von $\sigma$ geteilt. Die Werte der Summenhäufigkeit sind nicht mehr direkt ablesbar. Um das zu ändern, kann die rechte y-Achse mit einer entsprechend skalierten Einteilung versehen werden. Dazu sind die folgenden Befehle notwendig,

set yrange [-3.0:3.0]
set y2range [0:1.0]
set ytics nomirror
set link y2 via norm(y) inverse invnorm(y)
set y2tics 0.1 format "%.2f" nomirror
set y2tics add (0.01, 0.05, 0.95, 0.99)

mit denen die Skalierung der y2-Achse über die Verteilungsfunktion mit der y-Achse verknüpft wird. Zusätzlich sollten beide Achsen beschriftet werden.

set ylabel "sigma"
set y2label "relative Summenhäufigkeit"

Um die Ablesbarkeit der Werte aus dem Graphen zu erleichtern lässt sich mit

set grid xtics y2tics

noch ein Koordinatennetz hinzufügen. Dieses Netz, auf Papier ausgedruckt, wurde, als ,,Wahrscheinlichkeitspapier`` bezeichnet, in Vor-Computer-Zeiten für den schnellen Vergleich einer empirisch bestimmten Verteilung mit der Normalverteilung verwendet. Nun kann alles zusammen noch einmal neu gezeichnet werden.

plot "histogrammdata.txt" using 1:(invnorm($3/ntotal)) notitle,\
((x-mw)/std) with lines notitle;

Abbildung 5: Skalierte Darstellung der Summenhäufigkeit und der Verteilungsfunktion der Gauß-Verteilung auf ,,Wahrscheinlichkeitspapier``

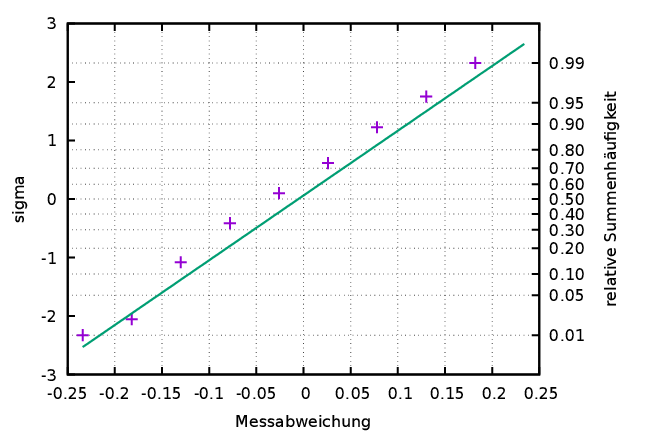Die in den Abbildung 4 und 5 eingezeichnete Gerade wurde auf Grundlage der am Anfang abgeschätzten Werte für $\mu$ und $\sigma$ berechnet. Es stellt sich nun die Frage, ob es nicht eine besser an die Datenpunkte angepasste Gerade gibt. Dazu kann wieder der Befehl stats verwendet werden. Nur wird er jetzt auf die Histogramm-Daten, auf die Spalten mit $\overline{x}$ und Summenhäufigkeit angewandt. Die Summenhäufigkeiten werden dabei mit der inversen Verteilungsfunktion (Gleichung 2) skaliert.

stats "histogrammdata.txt" using 1:(invnorm($3/ntotal));

Als Ergebnis erhält man neben den statistischen Informationen zu den Daten in den beiden Spalten auch Informationen zu den statistischen Beziehungen zwischen den beiden Datenspalten. Darunter auch die Parameter $a$ und $b$ der Geraden $y = a\, x + b$, die einen vorhandenen linearen Zusammenhang am besten beschreibt. Diese können mit den Befehlen

a=STATS_slope
b=STATS_intercept

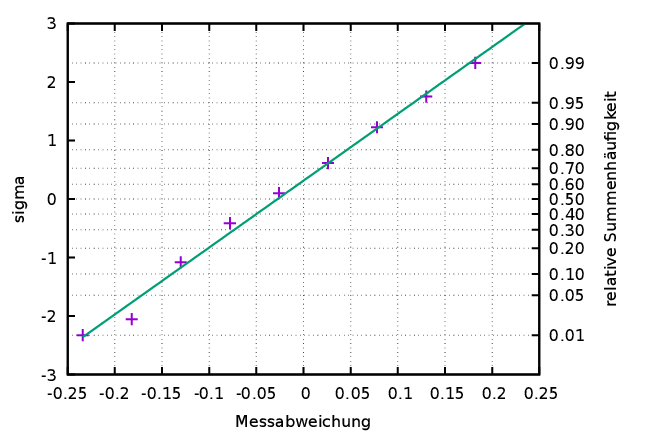
übernommen werden. Die Graphik wird mit der angepassten Geraden

y(x)=a*x+b

erneut gezeichnet (Abbildung 6).

plot "histogrammdata.txt" using 1:(invnorm($3/ntotal)) notitle, \
y(x) with lines notitle;

Abbildung 6: Skalierte Darstellung der Summenhäufigkeit und der angepassten Verteilungsfunktion der Gauß-Verteilung auf ,,Wahrscheinlichkeitspapier``

Aus den beiden Parametern $a$ und $b$ lassen sich der Mittelwerte $\mu$ und die Standardabweichung $\sigma$ der zugehörigen Normalverteilung bestimmen,

$$\mu = -\frac{b}{a} \hspace{5mm} \mathrm{und} \hspace{5mm} \sigma =\frac{1}{a}$$

und mit

print -b/a, 1/a

im Terminalfenster von GnuPlot ausgeben. Diese Werte sollten mit den am Anfang abgeschätzten Werten von $\mu$ und $\sigma$

print mw, std

im Rahmen der Fehlerintervalle, die auch in der Ausgabe des Befehls stats enthalten sind, übereinstimmen.

Literatur

Physikalisches Grundpraktikum: Einführungspraktikum
Mathematisch-Naturwissenschaftliche FakultätI der HUB
Institut für Physik 2007

http://gpr.physik.hu-berlin.de/Skripten/Einfuehrungspraktikum/PDF-Dateien/Einfuehrungspraktikum.pdf
abgerufen am 14.12.2016 9:49 Uhr

Physikalisches Grundpraktikum:
Einführung in die Messung, Auswertung und Darstellung experimenteller Ergebnisse in der Physik
Mathematisch-Naturwissenschaftliche Fakultät der HUB
Institut für Physik 2007

http://gpr.physik.hu-berlin.de/Skripten/Einfuehrung/PDF-Datei/Einfuehrung.pdf
abgerufen am 12.1.2017 11:57 Uhr

H.A.Sturges, The choice of a class interval
Journal of the American Statistical Association 21, 65-66 1926

D.W.Scott, On optimal and data-based histograms.
Biometrika 66, 605-610.1979