Can photons travel `faster than light'?
Marcus Chown
LIGHT cannot travel faster than it does in a vacuum. This, at any rate, is what Einstein postulated in 1905. Now, however, a physicist in East Germany claims that photons may be able to break this universal speed limit, known as c. The proposed effect, however, is very small indeed: the photons can exceed Einstein's limit by only one part in 1036.

K. Scharnhorst, of the Humboldt University in East Berlin, has made calculations using the theory of quantum electrodynamics, or QED, which describes how particles of light, or photons, interact with particles of matter - electrons and protons. His analysis of the vacuum, or empty space, reveals the possible existence of "faster-than-light" photons (Physics Letters B, vol 236, p 354).
QED predicts that the vacuum, far from being empty, seethes with short-lived, or virtual particles: pairs of electrons and positrons - their antiparticles - which come into existence and disappear again for fleetingly small intervals. These are known as vacuum fluctuations (New Scientist. Science. 2 December 1989).
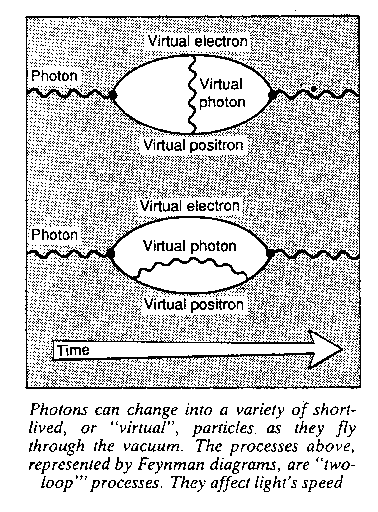
The apparent violation of the conservation of energy is permitted by Heisenberg's uncertainty principle, a cornerstone of quantum theory. Before they disappear, an electron and positron may exchange a "virtual" photon; alternatively, one of the particles may emit a "virtual" photon, then promptly reabsorb it. These are known to physicists as "two-loop" processes because Feynman diagrams that represent them contain two loops (see Figure above).
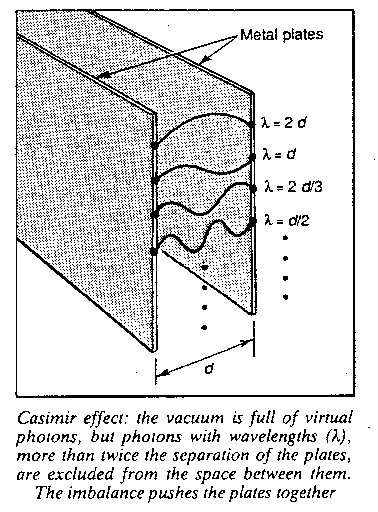
Scientists can observe the consequences of all these processes in the laboratory. One example is the Casimir effect, the result of a force that pulls together two closely-spaced metal plates.
Although in many circumstances photons behave as particles, they also have wave-like properties: in particular, they each have a wavelength associated with them. In effect, the plates exclude all virtual photons with wavelengths longer than twice the distance between the plates, technically because they do not satisfy the "boundary conditions" imposed by the theory of electromagnetism. The imbalance causes the plates to be pushed together (see Figure right).
Vacuum fluctuations also affect light as it travels through the vacuum. This is because, in flight, a tiny fraction of the photons spontaneously create virtual electron-positron pairs, which quickly annihilate each other to leave a photon. Two-loop processes also take place. All these contribute to the speed we measure for light in a vacuum.
Scharnhorst suggests that if the vacuum is modified, it may be possible to change the speed of light to more than its value in the vacuum. Such a modification can be brought about by bringing together two large conducting plates, as in the Casimir effect, and excluding some virtual photons.
This means that when photons travel between the plates, they cannot undergo two-loop processes that involve the excluded virtual photons. One would expect that the photons would spend a smaller fraction of their flight time undergoing two-loop processes than they would in a vacuum and so would travel marginally faster than they would in the vacuum.
In fact, detailed calculations are necessary to determine whether this is true. Scharnhorst has done the calculations and finds that it is. For photons travelling perpendicularly between the plates separated by 1 micrometre, the speed of light is increased by about one part in 1036 over its value in the vacuum. However, this effect is too small to be measured by any experiment.
Paul Davies of the University of Newcastle says that if photons could travel faster than the speed of light in a vacuum, it would have profound implications for physics. Many paradoxes would rear their ugly heads. In particular, events could violate "causality", that is, an effect could occur before its cause. For this reason, he strongly suspects that the Universe will conspire to make Scharnhorst's effect unobservable.
Davies says that in order to observe the effect, physicists would have to time a photon as it travelled across a short distance. They would have to measure as precisely as possible the time a photon is emitted by a source and then absorbed by a detector.
But atomic processes in the source and detector would be subject to Heisenberg's uncertainty principle, which means there will be an uncertainty in both the time of emission and absorption. These uncertainties will be greater than the time interval physicists must measure in order to confirm Scharnhorst's tiny increase in the speed of light.
One way to beat the uncertainty principle would be to use high energy photons, with correspondingly high-frequency. But then there is another problem, says Davies. The boundary conditions at the metal plates no longer apply at the energies required.
Davies concludes therefore that
Scharnhorst's result "does not imply the
breakdown of causality". 
Speed of light
The question of photons travelling "faster than light" (Science, 7 April) is surely just a matter of terminology. The value which we call c, the absolute limit to observed speed, is the speed at which any particle with zero restmass (such as a photon) would travel in "free space".
We are familiar with situations where light travels slower than c, through air or glass, for example, and this is the reason for refraction. All that is really being said is that true "free space" probably does not exist, and that what we call a vacuum has a tiny, but non-zero, refractive index, due to its being filled with virtual matter.
It is slightly misleading to call c the "speed of light": it can cause great confusion, for example, when trying to describe Cerenkov radiation (radiation emitted by a particle which travels through a medium faster than the speed of light in that medium).
I suppose we're stuck with it though, unless someone can come up with a catchy alternative. We have to get clear that c is a theoretical limit to speed, determined by the basic properties of the Universe. It just happens also to be the speed at which light would travel, if only it had the luxury of completely unobstructed path.
Tim Bierman, London, NW4