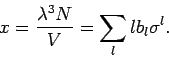Nächste Seite: Statistische Theorie dichter Fluide
Aufwärts: Systeme Wechselwirkender Teilchen
Vorherige Seite: Systeme Wechselwirkender Teilchen
Klassisches Bild, wechselwirkende Teilchen. Clusterentwicklung als
Ausgangspunkt für die Näherungsverfahren (MAYER,1937)
Modell: Einatomiges klassisches Gas, symmetrische Paarwechselwirkung
zwischen den Teilchen:
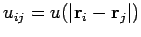 . Die Hamilton-Funktion des System lautet
. Die Hamilton-Funktion des System lautet
Zustandssumme:
mit
Für das ideale Gas (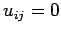 ) sind alle Exponentialfunktionen
) sind alle Exponentialfunktionen
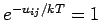 und
und
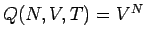 , so dass
, so dass
wie bereits diskutiert. Um die Abweichungen vom idealen Gas zu erfassen,
ist es zweckmässig die Funktionen
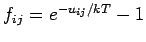 einzuführen (Mayer-Funktionen). Die Funktion
einzuführen (Mayer-Funktionen). Die Funktion 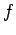 ist klein wenn
ist klein wenn 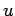 klein oder
klein oder 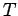 groß ist, und ist somit eine brauchbare Größe für eine
Hochtemperaturentwicklung. Es ergibt sich
groß ist, und ist somit eine brauchbare Größe für eine
Hochtemperaturentwicklung. Es ergibt sich
so dass 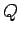 zerfällt in eine Summe verschiedener Integrale vom Typ
zerfällt in eine Summe verschiedener Integrale vom Typ
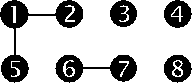
Diese Integrale lassen sich graphisch darstellen.
Das ist z.B. die Darstellung eines Integrals
(hier 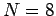 , die Kreise notieren die Teilchen, die Linien die
berücksichtigten
Wechselwirkungen, d.h. die
, die Kreise notieren die Teilchen, die Linien die
berücksichtigten
Wechselwirkungen, d.h. die 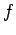 -Funktionen). Dieses Integral kann in ein
Produkt unabhängiger Integrale faktorisiert werden:
-Funktionen). Dieses Integral kann in ein
Produkt unabhängiger Integrale faktorisiert werden:
oder graphisch:
Die durch Linien (Wechselwirkung) verbundenen Teile dieser graphischen
Darstellung bezeichnet man als Cluster. Die Cluster-Darstellung vereinfacht die
Auswertung der Integrale, da die Cluster gleicher Struktur den gleichen
(multiplikativen) Beitrag zu allen Integralen liefern:
Alle Einteilchenbeiträge sind
Die Beiträge der Paare sind
u.s.w.
Sei 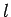 die Anzahl der Teilchen eines Clusters. Man definiert das
Cluster-Integral
die Anzahl der Teilchen eines Clusters. Man definiert das
Cluster-Integral
Z.B. für 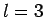 sind es 4 Cluster. Die Werte
sind es 4 Cluster. Die Werte 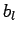 sind dimensionslos
und (im Grenzfall
sind dimensionslos
und (im Grenzfall
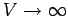 ) volumenunabhängig. Beispiele:
) volumenunabhängig. Beispiele:
(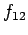 unterscheidet sich von Null nur in einem kleinem Bereich; Übergang zu der Relativkoordinaten und Koordinaten des
Massenschwerpunktes).
unterscheidet sich von Null nur in einem kleinem Bereich; Übergang zu der Relativkoordinaten und Koordinaten des
Massenschwerpunktes).
(der Übergang von der ersten zur zweiten Zeile entspricht der Einführung der Relativkoordinaten). Die zwei Summanden in der dritten
Zeile entsprechen den sog. irreduziblen Beiträgen.
Das Konfigurationsintegral 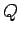 für ein
für ein 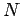 -Teilchensystem besteht aus
verschiedenen Kombinationen von Clusterintegralen. Nehmen wir an, das
Integral
-Teilchensystem besteht aus
verschiedenen Kombinationen von Clusterintegralen. Nehmen wir an, das
Integral 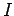 aus
aus 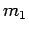 1-Cluster,
1-Cluster, 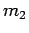 2-Cluster,
2-Cluster, 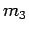 3-Cluster, u.s.w besteht, so dass
3-Cluster, u.s.w besteht, so dass
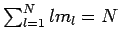 . Sei
. Sei 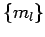 eine solche Zerlegung. Anzahl der Realisierungen einer solchen Zerlegung ist
eine solche Zerlegung. Anzahl der Realisierungen einer solchen Zerlegung ist
(um das zu sehen, teilen wir zuerst das System in
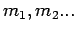 ''Boxen''
auf. Insgesamt
gibt es
''Boxen''
auf. Insgesamt
gibt es 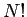 Plazierungen unterscheidbarer Moleküle. Innerhalb einer
Box gibt es
Plazierungen unterscheidbarer Moleküle. Innerhalb einer
Box gibt es 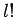 Permutationen, für alle
Permutationen, für alle 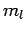
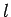 -Boxen also
-Boxen also
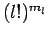 ; die Boxen gleicher Größe sind nicht unterscheidbar,
daher gibt es noch
; die Boxen gleicher Größe sind nicht unterscheidbar,
daher gibt es noch 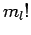 Permutationen). Der Gesamtausdruck für
Permutationen). Der Gesamtausdruck für
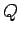 ist also
ist also
Die gesamte Zustandssumme ist
mit der Nebenbedingung
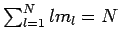 . Die Nebenbedingung ist sehr
störend, kann aber durch einen Übergang zu einem großkanonischen
Ensemble vermieden werden. Die großkanonische Zustandssumme
. Die Nebenbedingung ist sehr
störend, kann aber durch einen Übergang zu einem großkanonischen
Ensemble vermieden werden. Die großkanonische Zustandssumme
mit
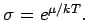 Mit
Mit
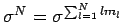 folgt:
folgt:
Die Summation in der 1. Zeile ist eingeschränkt durch die Nebenbedingung
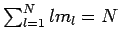 , die Summation in der 2. Zeile ist hingegen frei!
Der letzte Ausdruck kann weiter umgeformt werden:
, die Summation in der 2. Zeile ist hingegen frei!
Der letzte Ausdruck kann weiter umgeformt werden:
Damit ist (da
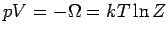 ):
):
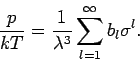 |
(12) |
Für die mittlere Teilchenzahl
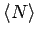 gilt:
gilt:
Somit
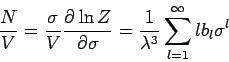 |
(13) |
Die Zustandsgleichung ergibt sich durch das Eliminieren der Fugazität 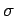 aus Gl.(12) und (13). Daraus folgt die
Virialenwicklung
aus Gl.(12) und (13). Daraus folgt die
Virialenwicklung
Die Koeffizienten der Entwicklung nach Potenzen von 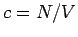 sind die
Virialkoeffizienten
sind die
Virialkoeffizienten
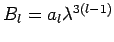 (die Virialkoeffizienten
(die Virialkoeffizienten 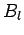 haben die Dimension der Potenzen des Volumens).
haben die Dimension der Potenzen des Volumens).
Die Koeffizienten 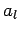 können durch
können durch 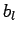 ausgedruckt werden:
ausgedruckt werden:
so dass der 2. Virialkoeffizient ist
![\begin{displaymath}
B_{2}=2\pi \int_{0}^{\infty }\left[ 1-e^{-u(r)/kT}\right] r^{2}dr.
\end{displaymath}](img562.png) |
(15) |
Für ein Gas harter Kugeln vom Radius 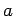 gilt
gilt
und
Bemerkung: Die Gl.(14) kann auf folgendem Wege
hergeleitet werden: Führen wir ein
Betrachten wir dann die Reihenentwicklung von 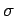 nach Potenzen von
nach Potenzen von
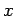 :
:
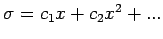 . Aus Gl.(13) dann folgt:
. Aus Gl.(13) dann folgt:
Durch Vergleich der Koeffizienten erhalten wir:
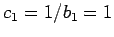 ,
,
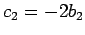 ,
,
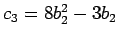 . Die Koeffizienten
. Die Koeffizienten 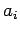 der
Entwicklung von
der
Entwicklung von
sind
dann durch Gl.(14) gegeben.



Nächste Seite: Statistische Theorie dichter Fluide
Aufwärts: Systeme Wechselwirkender Teilchen
Vorherige Seite: Systeme Wechselwirkender Teilchen
Prof. Igor Sokolov
2004-07-01
![]() . Die Hamilton-Funktion des System lautet
. Die Hamilton-Funktion des System lautet
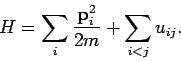
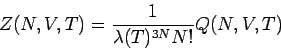
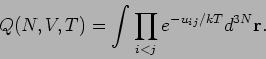
![\begin{eqnarray*}
Q &=&\int \prod_{i<j}(1+f_{ij})d^{3N}\mathbf{r=} \\
&=&\int \...
...{ij}f_{kl}+...\right] d^{3}\mathbf{r}_{1}...d^{3}\mathbf{r}_{N},
\end{eqnarray*}](img510.png)
![\begin{displaymath}
\left[ \bullet \right] =\int_{V}d^{3}\mathbf{r}=V
\end{displaymath}](img517.png)
![]() die Anzahl der Teilchen eines Clusters. Man definiert das
Cluster-Integral
die Anzahl der Teilchen eines Clusters. Man definiert das
Cluster-Integral
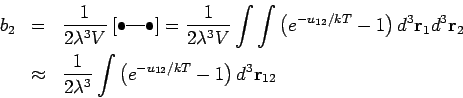
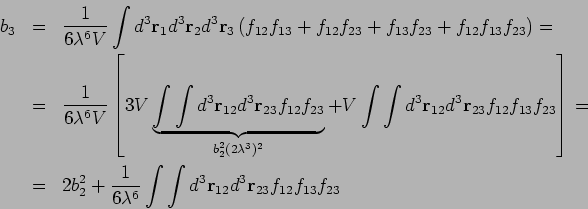
![]() für ein
für ein ![]() -Teilchensystem besteht aus
verschiedenen Kombinationen von Clusterintegralen. Nehmen wir an, das
Integral
-Teilchensystem besteht aus
verschiedenen Kombinationen von Clusterintegralen. Nehmen wir an, das
Integral ![]() aus
aus ![]() 1-Cluster,
1-Cluster, ![]() 2-Cluster,
2-Cluster, ![]() 3-Cluster, u.s.w besteht, so dass
3-Cluster, u.s.w besteht, so dass
![]() . Sei
. Sei ![]() eine solche Zerlegung. Anzahl der Realisierungen einer solchen Zerlegung ist
eine solche Zerlegung. Anzahl der Realisierungen einer solchen Zerlegung ist
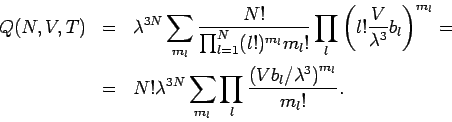
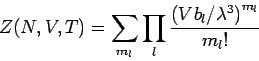
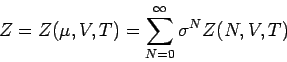
![\begin{eqnarray*}
Z &=&\sum_{N=0}^{\infty }\sum_{\left\{ m_{l}\right\} }\left[ \...
... V\sigma ^{l}b_{l}/\lambda ^{3}\right) ^{m_{l}}}{m_{l}!}\right]
\end{eqnarray*}](img542.png)
![\begin{eqnarray*}
Z &=&\sum_{m_{1},m_{2},...=0}^{\infty }\left[ \prod_{l=1}^{\in...
...m_{l=1}^{\infty }\frac{V\sigma ^{l}b_{l}}{\lambda
^{3}}\right] .
\end{eqnarray*}](img543.png)
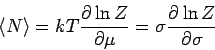

![]() können durch
können durch ![]() ausgedruckt werden:
ausgedruckt werden: