


Nächste Seite: Ising-Modell und verwandte Gittermodelle.
Aufwärts: Phasenübergänge
Vorherige Seite: Phasenübergänge
Prominentestes Beispiel: Ferromagnetismus. Magnetmoment des Elektrons
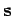 - Spinvariable (
- Spinvariable (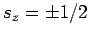 ),
), 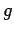 - Landé-Faktor,
- Landé-Faktor,
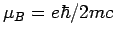 - Bohrsches Magneton. Der Modell-Hämiltonian eines Spinsystems:
- Bohrsches Magneton. Der Modell-Hämiltonian eines Spinsystems:
( - Magnetfeld, gibt
- Magnetfeld, gibt 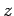 -Richtung vor).
-Richtung vor). 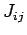 -
Austauschintegral
-
Austauschintegral
(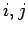 numerieren die Atome,
numerieren die Atome, 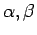 - die Koordinatenkomponenten;
- die Koordinatenkomponenten; 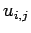 ist die effektive Wechselwirkung, dieses effektive Potential zeigt
einen Coulomb-artigen Abfall), so dass
ist die effektive Wechselwirkung, dieses effektive Potential zeigt
einen Coulomb-artigen Abfall), so dass 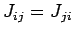 ,
, 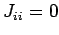 .
. 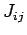 fällt sehr schnell mit dem Abstand zwischen den Atome ab, man kann oft
annehmen, dass
fällt sehr schnell mit dem Abstand zwischen den Atome ab, man kann oft
annehmen, dass 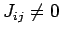 nur wenn entsprechende Atome nächste
Nachbarn im Kristallgitter sind.
nur wenn entsprechende Atome nächste
Nachbarn im Kristallgitter sind.
Wenn die Wechselwirkung isotrop ist, entspricht unser Hamiltonian den
HEISENBERG-Modell (gutes Modell für magletische Isolatoren,
sieh nolting, §4.3.6.).
Wenn 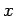 - und
- und 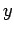 -komponenten der WW verhachlässigt werden können,
folgt dann
-komponenten der WW verhachlässigt werden können,
folgt dann
In diesem Fall spielen die Kommutationseigenschaften der Spin 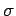 -Matrizen keine Rolle, das Modell ist im Grunde genommen klassisch. Diese
Form des Hamilton-Operators definiert das ISING-Modell (W. Lenz,
1920, E. Ising, 1925), das erfolgreichste Modell der statistischen Physik
überhaupt! Das ist ein vernünftiges Modell für stark anisotrope
Ferro- oder Antiferromagneten:
-Matrizen keine Rolle, das Modell ist im Grunde genommen klassisch. Diese
Form des Hamilton-Operators definiert das ISING-Modell (W. Lenz,
1920, E. Ising, 1925), das erfolgreichste Modell der statistischen Physik
überhaupt! Das ist ein vernünftiges Modell für stark anisotrope
Ferro- oder Antiferromagneten:
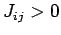 : Zustand : Zustand
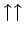 wird bevorzugt (eventuel
Ferromagnetismus) wird bevorzugt (eventuel
Ferromagnetismus) |
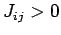 : Zustand : Zustand
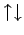 wird bevorzugt (eventuel
Antiferromagnetismus) wird bevorzugt (eventuel
Antiferromagnetismus) |
Wenn die 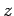 -Komponente der WW vernachlässigt wird, und die
-Komponente der WW vernachlässigt wird, und die 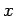 - und
- und 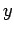 -komponenten anisotrope Beiträge zu
-komponenten anisotrope Beiträge zu 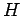 liefern, folgt
liefern, folgt
(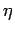 beschreibt die Stärke der Anisotropie). Das ist das XY-Modell
(keine unmittelbare experimenelle Entsprechung, aber von theoretischen
Interesse). In weiterem betrachten wir nur klassische Modelle.
beschreibt die Stärke der Anisotropie). Das ist das XY-Modell
(keine unmittelbare experimenelle Entsprechung, aber von theoretischen
Interesse). In weiterem betrachten wir nur klassische Modelle.



Nächste Seite: Ising-Modell und verwandte Gittermodelle.
Aufwärts: Phasenübergänge
Vorherige Seite: Phasenübergänge
Prof. Igor Sokolov
2004-07-01
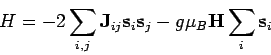
![]() - und
- und ![]() -komponenten der WW verhachlässigt werden können,
folgt dann
-komponenten der WW verhachlässigt werden können,
folgt dann
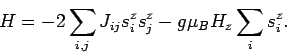
![]() -Komponente der WW vernachlässigt wird, und die
-Komponente der WW vernachlässigt wird, und die ![]() - und
- und ![]() -komponenten anisotrope Beiträge zu
-komponenten anisotrope Beiträge zu ![]() liefern, folgt
liefern, folgt
![\begin{displaymath}
H=-2\sum_{i,j}J_{ij}\left[ \left( 1+\eta _{ij}\right)
s_{i}^...
...^{x}+\left( 1-\eta _{ij}\right) s_{i}^{y}s_{j}^{y}\right] -...
\end{displaymath}](img730.png)