Übungen zur Physik für Chemiker I
Wintersemester 2008/2009
Aufgaben zur 11. Übung am 20.01.09
Rotationsenergie, Drehimpuls und Kreisel
51. Energie eines Wirbelsturmes
Ein Wirbelsturm lässt sich näherungsweise als ein gewaltiger rotierender Luftzylinder auffassen. Sein Durchmesser betrage 60 km, seine Höhe 6 km. Am äußeren Rand herrsche eine Windgeschwindigkeit von 180 km/h. Berechnen Sie die im Wirbelsturm gespeicherte Energie und vergleichen Sie diese mit der jährlichen Energieerzeugung eines Kernkraftwerkes von 1000 MW Leistung!
52. Drehimpuls
Nach dem Rutherford - Bohr’schen Atommodell „besteht“ ein Wasserstoffatom aus einem Proton als Atomkern und einem Elektron, welches den Atomkern umkreist. Das Elektron (Masse me = 9,1.10-31 kg) hat im Grundzustand die kinetische Energie EK1 = 2,18.10-18 J und einen Bahndrehimpuls L1 = 1,05.10-34 Js. Man bestimme den Radius r1 des Wasserstoffatoms.
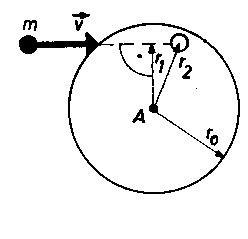
53. Unelastischer Drehstoss
Ein homogener
hölzerner Vollzylinder habe die Masse mZ und den Radius ro
und sei um die Zylinderachse drehbar gelagert. In den ruhenden Zylinder dringt
das Geschoss (mG) einer Pistole ein. Die Geschossbahn verläuft
senkrecht zur Achse und hat den Abstand r1 von ihr. Das Geschoss
bleibt im Abstand r2 von der Achse stecken. Nach dem Einschuss dreht
sich der Zylinder mit der Frequenz f. Berechnen Sie die Geschwindigkeit v, die
das Geschoss unmittelbar vor dem Eindringen hatte!
mZ = 600 g ; mG
= 5,0 g ; ro = 50 mm ; r1
= 30 mm ; r2 = 35 mm ; f = 2,5 s-1
54. Präzession
Ein Kreisel ist bezüglich des Drehpunktes A im Gleichgewicht mit dem Gegengewicht. Der Kreisel hat die Drehfrequenz f. Wird ein Zusatzgewicht der Masse m in der Entfernung l vom Drehpunkt A angehängt, so stellt sich eine Präzessionsfrequenz fp ein. Der Vektor wp ist nach oben gerichtet.
· Welche Richtung hat der Drehimpulsvektor des Kreisels?
· Wie groß ist das Trägheitsmoment JS des Kreisels?
l = 20,0 cm ; f = 200 s-1
; fP = 0,10 s-1 ; m = 50 g

55. Rotation eines Stickstoffmoleküls
Der
Gleichgewichtsabstand zwischen den Atomkernen des N2-Moleküls
beträgt a = 0,11 nm. Die Masse eines Stickstoffkerns ist mN = 14 u
(atomare Einheiten) mit u = 1,66.10-27 kg. Es sollen die
Energien der drei niedrigsten Drehimpulszustände des Stickstoffmoleküls mit ![]() für (l = 1,2,3 und
für (l = 1,2,3 und ![]() ) berechnet werden:
) berechnet werden:
a) Fassen Sie das Molekül als Hantel mit zwei gleichen Punktmassen auf und berechnen Sie das Trägheitsmoment J bei Rotation um eine Achse, die senkrecht auf der Verbindungslinie der N-Atome steht und durch den Schwerpunkt des Moleküls verläuft.
b) Berechnen Sie die Energieniveaus der Rotationszustände mittels der Beziehung
