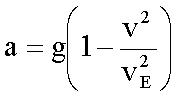Numerische Integration der
Bewegungsgleichung
Das Eulerverfahren
Die Aufstellung der
Bewegungsgleichung liefert einen Ausdruck der Form
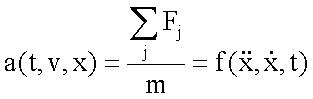
Dies ist eine
Differentialgleichung zweiter Ordnung, die u. U. nicht geschlossen integriert
werden kann. Man ist somit auf numerische Lösungsverfahren angewiesen.
Eine einfache
Integrationsmethode nach Euler nutzt die Definition der Größen Beschleunigung
und Geschwindigkeit:
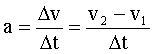 sowie
sowie ![]()
Ausgehend von einem
Anfangswert für v(t=t0) = v0 und x(t=t0) = x0
erhält man für hinreichend kleine Zeitintervalle Δt schrittweise
Geschwindigkeit und Weg aus der Beschleunigung:
![]() und
und ![]()
![]()
Allgemein gelten dann
folgende Rekursivformeln (tn = nΔt+t0):
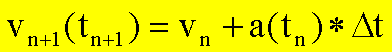
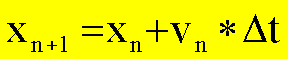
Das Eulerverfahren ist nur
für sehr kleine Zeitschritte hinreichend genau. Will man bessere Resultate,
kann man z.B. das Runge-Kutta Verfahren anwenden.
Beispiel – Freier Fall mit Luftreibung
Geschwindigkeitsabhängige
Beschleunigung bei Endgeschwindigkeit vE: