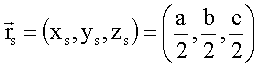Dichte und Massenschwerpunkt

Gegeben sei ein Körper der Gesamtmasse M, welche das Volumen V einnimmt. Wir zerlegen gedanklich den Körper in kleine Massenelemente Dm = m_i, die das Volumen DV = V_i einnehmen:

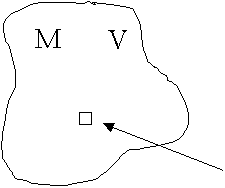
Es gilt dann

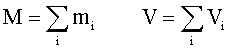
Als Dichte definiert man den Grenzübergang

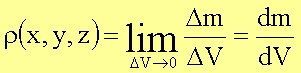
Im allgemeinen ist die Dichte eine Funktion der Koordinaten des Körpers. Ist der betreffende Körper homogen, so kann man vom Differential zum Verhältnis r = m/V übergehen. Ist umgekehrt die ortsabhängige Dichte eines Körpers bekannt, so kann die Gesamtmasse mittels

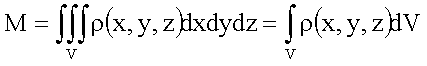
berechnet werden.

Gehen wir in der Definition des Massenschwerpunktes

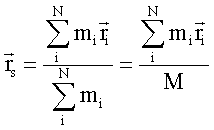
zum kontinuierlichen Körper über, so folgt

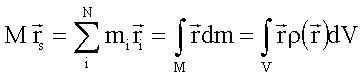
In homogenen Körpern kann die Dichte vor das Integral gezogen werden und die Integration über das Volumen vereinfacht sich zu

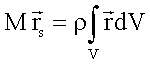
bzw.

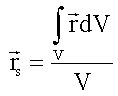
In diesem Fall eines homogenen Körpers hängt der Massenschwerpunkt nur von seiner Geometrie ab. Für einen Quader der Seitenlängen a,b,c gilt z.B.

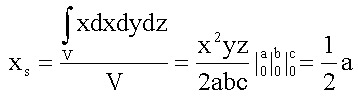
Analog findet man für die beiden anderen Komponenten b/2 und c/2.

Also gilt: