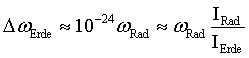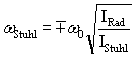Drehstuhlexperiment I

Im Versuch wird ein rotierendes Rad mit der Kreisfrequenz und dem Trägheitsmoment einer Person auf einem Drehstuhl mit dem Gesamtträgheitsmoment (einschließlich Person) und der Anfangskreisfrequenz

übergeben. Die Drehachse des Rades zeigt zu Beginn senkrecht zum Schwerkraftvektor.

Wir zerlegen den Gesamtdrehimpuls in eine Komponente parallel zur Schwerkraft und einen zweiten Vektor senkrecht zur Schwerkraft.

Allgemein gilt für jede Komponente von :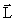

Im zu beschreibenden Experiment wird das rotierende Rad der Versuchsperson auf dem Stuhl so übergeben, dass die Radachse senkrecht zur Stuhlachse zeigt. Der Stuhl ist zunächst fixiert, so dass sich der gesamte Drehimpuls im Rad befindet. Nach Loslassen des Stuhles ändert sich zunächst nichts. Es gelten also folgende Anfangsbedingungen:

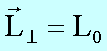
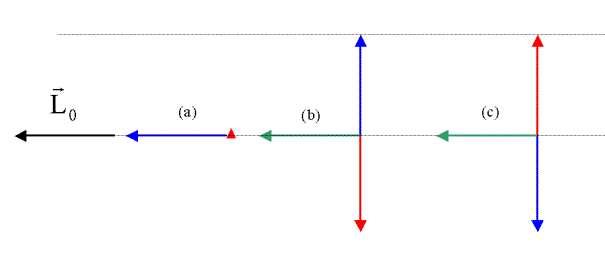
Jetzt wird das Rad einmal um 90° gedreht (Radachse parallel zur Stuhlachse) und danach um -90° (Radachse antiparallel zur Stuhlachse):

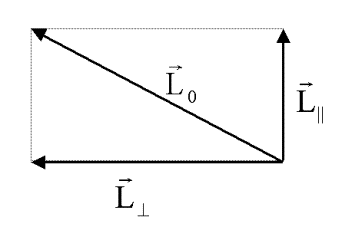
roter Vektor:	Drehimpuls des Stuhles (mit Person)
blauer Vektor:	Parallele Drehimpulskomponente des Rades
grüner Vektor:	Senkrechte Drehimpulskomponente
grüner Punkt:	Kennzeichnung der rechten Hand.

Die Drehzahl des Stuhles erhöht sich kontinuierlich bei Kippung des Rades. Durch die Drehung des Stuhles wird der Drehimpuls des Rades kompensiert. Stellt man die Achse von parallel zu antiparallel, kehrt sich die Drehrichtung um. Insgesamt bleibt die parallele Drehimpulskomponente immer gleich Null. Die Zunahme der Drehzahl wird gut durch die Bildunschärfe der Hand verdeutlicht.

±90°-Drehung

Der Drehimpulserhaltungssatz liefert:

Der Energieerhaltungssatz fordert

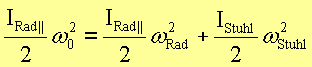
Wird das Rad in die Vertikale gedreht, so geht Rotationsenergie des Rades auf Rotationsenergie des Stuhles über. Dabei ist das Trägheitsmoment des Rades zu berücksichtigen, welches bei Rotation um die Stuhlachse ebenfalls Energie aufnimmt. Das Rad mit dem Trägheitsmoment bei Rotation um die Radachse wird also langsamer.

Die Drehzahl des Stuhles folgt direkt aus dem Drehimpulserhaltungssatz. Wir substituieren mittels des Drehimpulssatzes im Energiesatz und erhalten dann die Kreisfrequenz des Rades:

Besitzen Rad und Stuhl das gleiche Trägheitsmoment, so haben beide Objekte die entgegengesetzt gleiche Drehzahl w₀/Ö2. Die Energie teilt sich hälftig auf Stuhl bzw. Rad auf. Die maximal erreichbare Drehzahl des Stuhles kann sogar überliegen, falls sein Trägheitsmoment geringer, als der des Rades sein sollte. Normalerweise ist jedoch . Die Drehzahl des Rades ändert sich nur unwesentlich.

Im Falle einer Drehung der Radachse von ±90° muss die Drehimpulskomponente in senkrechter Richtung erhalten bleiben. (siehe grüne Pfeile in obiger Abbildung). Während in paralleler Richtung die Drehbewegung von der Unterlage entkoppelt ist (jedenfalls nahezu bei idealer Lagerung), tritt in vertikaler Richtung eine Drehimpulskopplung mit dem Erdball auf (wäre der Stuhl kardanisch gelagert, würde er sich nunmehr entsprechend L₀ um seine Vertikalachse zu drehen beginnen):

Wegen des riesigen Massenträgheitsmomentes der Erde ist ihre Drehimpulsänderung, die den Drehimpuls des Rades aufnimmt, zwar gleich groß, führt aber zu einer vernachlässigbaren Drehzahländerung: