Lösung der Bewegungsgleichung für

erzwungene, gedämpfte Schwingungen

Wir hatten die Gleichung

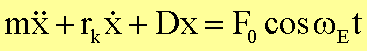
Mit den Abkürzungen

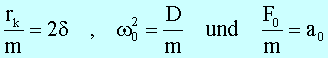
erhalten wir

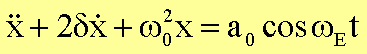
Hierin bedeuten die Eigen(kreis)frequenz des Oszillators, die Erreger(kreis)frequenz, d das logarithmische Dekrement, welches die Stärke der Dämpfung beschreibt) und a₀ die Beschleunigung des Oszillators durch die angreifende periodische Kraft. Um die Gleichung lösen zu können, ersetzen wir die Kraft durch den komplexen Ausdruck :

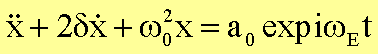
Dies ermöglicht den ebenfalls komplexen Lösungsansatz

Da die angreifende Kraft eine reelle Größe ist, interessiert als Lösung auch nur der Realteil des Ansatzes . Der komplexe Ansatz ermöglicht jedoch das Lösen der Differentialgleichung.

Mit

erhalten wir

und

Einsetzen in die Ausgangsgleichung und Division durch expiw_Et liefert:

bzw.

Diese Beziehung wird aufgeteilt in eine Gleichung für den Realteil und eine Gleichung für den Imaginärteil:

Aus diesem Gleichungssystem können die Amplitude x_A und der Phasenwinkel a in Abhängigkeit von der Erregerfrequenz bestimmt werden. Unter Ausnutzung von sin²a = 1 - cos²a folgt für die Amplitude:

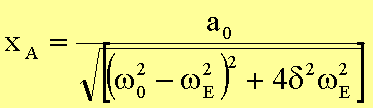
Division beider Gleichungen ergibt den Phasenwinkel

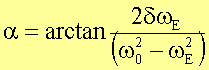
Darstellung der Lösung in der komplexen Ebene

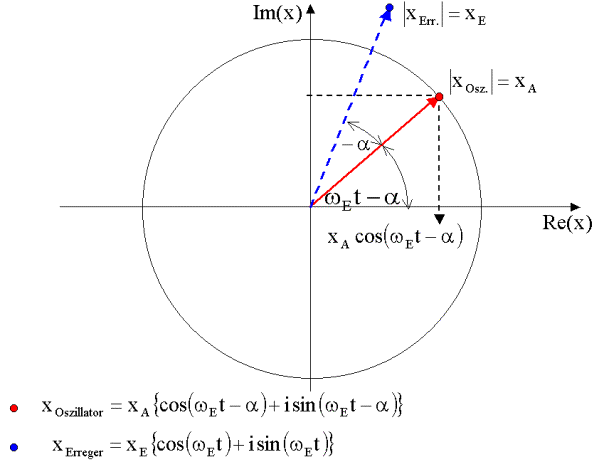
Die komplexe Exponentialfunktion kann als Zeiger in einem Polardiagramm (Zeigerdiagramm) dargestellt werden, der den Betrag x_A und den Phasenwinkel w_Et-a hat.

· Die Elongation des Oszillators ergibt sich aus dem Realteil von x ( Re(x) ).

· Die Phase des Oszillators erhält man aus dem Verhältnis von Imaginär- zu Realteil.