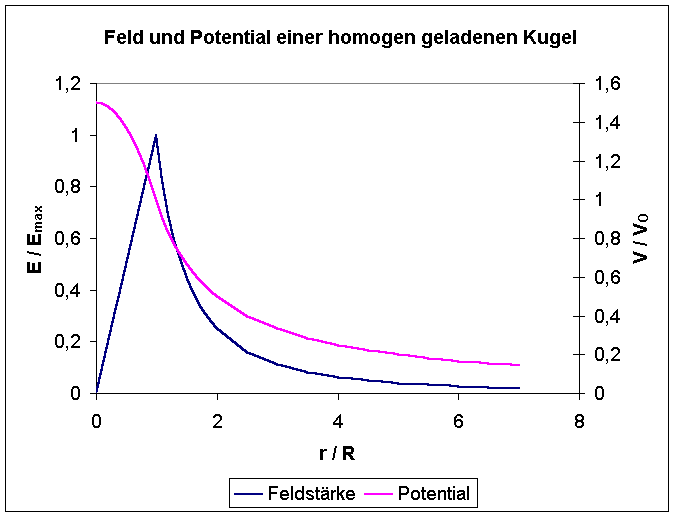
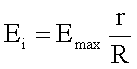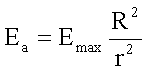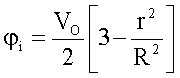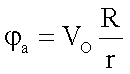Feld und Potential einer homogen geladenen Kugel

Es gilt der Gauß’sche Satz:

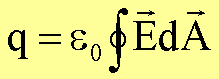
Die Größe q ist dabei die innerhalb der geschlossenen Fläche A befindliche Ladung.

· Außenraum der geladenen Kugel

Wir legen um die Gesamtladung q = Q eine geschlossene Kugelfläche der Oberfläche

Aus Symmetriegründen kann das elektrische Feld nur noch von r abhängen, während dA auch eine Funktion der Winkel j und J ist:

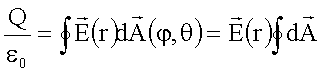
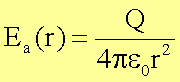
Führt man die Volumenladungsdichte

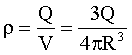
ein, so erhält man mittels

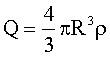
auch

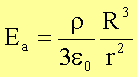
· Innenraum der homogen geladenen Kugel

Tritt man in das Innere der Kugel ein, so ergibt sich die innerhalb der Integrationsfläche befindliche Ladung bei konstanter Ladungsdichte zu

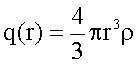
mit r < R.

Das elektrische Feld im Kugelinneren ergibt sich damit zu

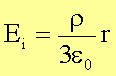
bzw.

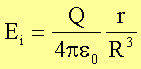
· Das Potential der geladenen Kugel

Das Potential bzw. die potentielle Energie j der Kugel berechnet man mittels

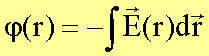
· r > R

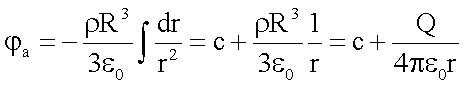
Mit erhält man c = 0.

· r < R

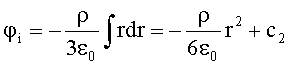
Wegen der Stetigkeit des Potentials an der Kugeloberfläche

erhält man für die Integrationskonstante c₂:

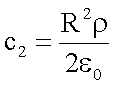
Damit ist das Potential im Innenraum:

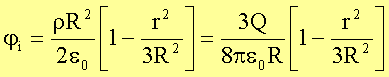
Mit

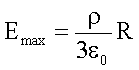und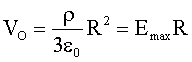

erhält man folgende Übersicht:

	r <= R	r >= R
E
j