Das Trägheitsmoment

Ein Körper rotiert um eine Achse A. Welche Bewegungsenergie hat er gespeichert?

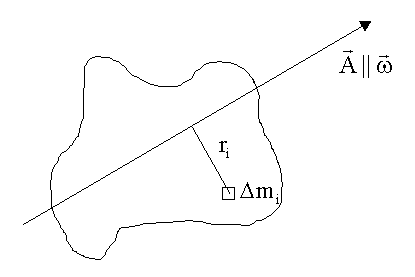
Wir zerlegen den Körper in Massenelemente . Jedes Massenelement, das im Abstand um die Achse A mit der Winkelgeschwindigkeit w rotiert, hat die Energie

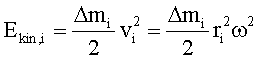
Aufsummation aller Beiträge ergibt die Rotationsenergie

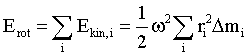
Im Falle kontinuierlicher Massenverteilungen geht man von der Summe zum Integral über:

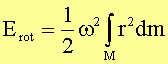
Das Integral

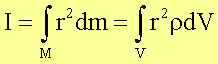
bezeichnet man als Massenträgheitsmoment eines Körpers bezüglich seiner Rotationsachse A. Damit kann die Rotationsenergie ausgedrückt werden als

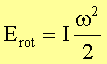
Die Berechnung eines beliebigen Trägheitsmomentes kann mit Hilfe des Steiner’schen Satzes auf die Berechnung des Trägheitsmomentes bezüglich einer Achse durch den Schwerpunkt zurückgeführt werden:

Das Trägheitsmoment eines Körpers bei Rotation um eine beliebige Achse B ist gleich dem Trägheitsmoment des Körpers bei Rotation um eine zu B parallele Achse, die durch den Schwerpunkt verläuft, zuzüglich des Trägheitsmomentes der im Schwerpunkt vereinigten Masse bei Rotation um B.

Es sei 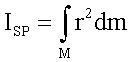das Trägheitsmoment bei Rotation um eine Achse durch den Schwerpunkt. Weiterhin sei a der Abstand zwischen der Achse B und der Achse durch den Schwerpunkt und R = r_B = r+a. Dann gilt:

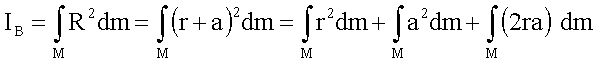
Wegen 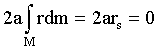( r_s – Schwerpunktkoordinate ) gilt:

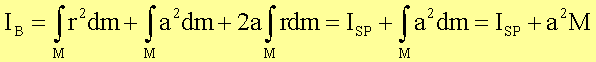
Für diskrete Massenverteilungen (insbesondere Punktmassenverteilungen) muss summiert werden:

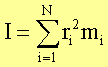
Beispiel: Trägheitsmoment eines zweiatomigen Moleküls bei Rotation um eine Achse durch den Schwerpunkt

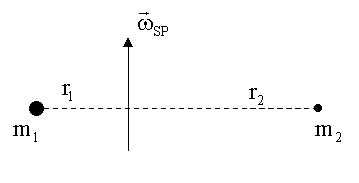
Durch Erweitern mit dem Faktor ( m₁ + m₂ ) formt man den Ausdruck um in

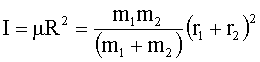
Hierin bedeuten µ die reduzierte Masse und R = r₁ + r₂ den Abstand der Atome im Molekül.