Stehende Längswellen in einer Gassäule

(Rubens’sches Flammenrohr)

Beim sogenannten Rubens’schen Flammenrohr wird vor einem Metallrohr (hier Messing) am offenen Ende zwecks Einkopplung einer Schallwelle ein Lautsprecher positioniert. Die Schallwelle breitet sich im Rohr aus und wird am abgeschlossenen „festen“ Ende reflektiert. Die Frequenz der Schallwelle und ihre Amplitude kann mittels eines Sinusgenerators verändert werden. Der Generator ist mit dem Lautsprecher verbunden.

Für bestimmte Frequenzen bilden sich im Rohr stehende Wellen aus. Am Ende des Rohres befindet sich ein Auslenkungsknoten, an der Einkoppelstelle ein Auslenkungsbauch. Die Amplitude des “Bauches“ wird bestimmt durch die Auslenkung der Lautsprechermembran.

Um die stehende Welle sichtbar zu machen, wird in das Rohr Gas eingelassen, welches durch kleine in regelmäßigen Abständen angebrachte Öffnungen an der Oberseite des Rohres entweichen kann. Die von unten einströmende Erdgasmenge wird so einreguliert, daß das aus den Löchern austretende und entzündete Gas etwa 5-8 cm hohe Flämmchen ergibt.

Position Amplituden(Auslenkungs-)knoten p = p₀

Position der Schallquelle – Einkopplung am offenen Ende

Bevor der Lautsprecher eingeschaltet wird, brennt das Gas mit gleich hohen Flammen. Dies ändert sich unwesentlich, wenn man die Schallquelle einschaltet. Durch Variation der Frequenz wird erreicht, dass das Flammenbild relative Maxima und Minima zeigt:

Wo innen im Rohr ständig ein zeitlich konstant hoher Druck herrscht (ein Auslenkungsknoten Dp = 0), brennen außen die Flammen hoch. Wo innen der Druck ständig wechselt (Auslenkungsbauch Dp>0) und damit das Gas an den Löchern ständig vorbeiströmt, brennen außen die Flammen niedrig (siehe Diskussion am Ende dieser Erörterung). Wir haben also folgende Zuordnung:

Auslenkungsknoten	Flammenhöhe rel. Maximum
Auslenkungsbauch	Flammenhöhe rel. Minimum

Für das oben gezeigte Flammenbild gelten folgende Parameter:

Frequenz / Hz	Abstand Maxima / m l/2	Rohrlänge l / m	Zahl der Halbwellen	Gasart
430 ± 10	0,52 ± 0,01	3,30	6	Erdgas

Der Abstand der relativen Flammenmaxima (Knoten der Schallwelle) entspricht der halben Wellenlänge 52 cm. Wir beobachten für 430 Hz insgesamt 6 Halbwellen zuzüglich einer Viertelwellenlänge am offenen Ende. In Rohren mit einem offenen und einem geschlossenen Ende können sich stehende Wellen mit folgenden Wellenlängen l_n ausbreiten:

bzw.

Setzen wir l = 3,3m und n = 6 in obige Gleichung ein, so folgt für die Wellenlänge 1,015m in guter Übereinstimmung mit dem gemessenen wert l = 1,04 m. Wir verwenden im weiteren den Mittelwert l = 1,03 m.

Aus gemessener Wellenlänge und Frequenz folgt die Schallgeschwindigkeit im Rohr zu

Die Schallgeschwindigkeit ist bestimmt durch die chemische Zusammensetzung des Gases. Luft ist es offensichtlich nicht (c @ 330 m/s).

Für elastische Wellen in Gasen erhielten wir durch Lösen der Wellengleichung die Relation

mit

Wir ermitteln den Kompressionsmodul unter Verwendung der Zustandsgleichung für ideale Gase (m- Gasmasse; µ-molare Masse):

bzw.

Differentiation ergibt k:

Wegen m/V = r verwenden wir die Zustandsgleichung in der Form:

Damit erhält man für den Kompressionsmodul eines idealen Gases:

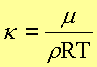
und damit für die Schallgeschwindigkeit:

Die Schallgeschwindigkeit verhält sich reziprok zur Wurzel aus der molaren Masse. Das Verhältnis zweier molarer Massen ist somit bestimmt durch das Verhältnis des Quadrates der Schallgeschwindigkeiten:

Wir erhalten für µ_Luft = 29g, c_Luft = 330 m/s und c_Gas = 443 m/s den Wert µ_Gas=16,1g. Damit haben wir nachgewiesen, dass Erdgas mit einer mittleren relative Molekülmasse µ_r =16 im wesentlichen aus Methan besteht.

Die Resultate unserer quantitativen Auswertung lauten also:

λn / m	c / ( m/s )	µr	Gas
1,03	443	16	Methan

Wir erörtern nachträglich den Zusammenhang zwischen Flammenhöhe und Auslenkung der Gasmoleküle.

Die Flammenhöhe bildet den Verlauf des statischen Druckes entlang des Rohres ab. Der statische Druck eines strömenden Gases in Rohren wird durch die Bernoulligleichung beschrieben:

Bernoulli-Gleichung:

Der Term ist der sogenannte Staudruck. Der statische Druck eines bewegten Mediums ist bei konstantem Gesamtdruck um den Betrag des Staudruckes reduziert (Sogeffekt). Ein strömendes Gas wird also an der Austrittsöffnung einen niederen Druck aufweisen, als ein ruhendes Gas.

Ein ruhendes Gas entspricht in der stehenden Welle den Schwingungsknoten. Die thermische Bewegung des Gases bleibt hierbei außer acht, da diese Bewegung isotrop, die Welle aber gerichtet ist. Die thermische Bewegung bewirkt einen Teilchenaustausch, die mittlere Geschwindigkeit

im Knoten ist jedoch gleich Null. Die Geschwindigkeit eines Gasteilchens hängt mit der Auslenkungsamplitude zusammen: . Für die Druckverhältnisse an einer Ausströmöffnung benötigen wir einen zeitlichen Mittelwert. Da für den Staudruck das Quadrat der Geschwindigkeit bestimmend ist, berechnen wir den zeitlichen quadratischen Mittelwert – den sogenannten Effektivwert. Für sinusartige Schwingungen gilt:

Allgemein gilt an jedem Punkt x des Rohres:

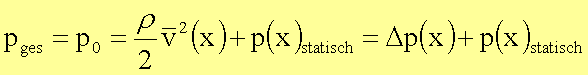
Damit wird der statische Druck reduziert um den durch die Gasbewegung bestimmten Staudruck:

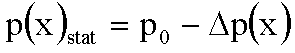
In einem Knoten gilt:

In einem Bauch wird die Druckschwankung bestimmt durch den maximalen Betrag der Druckschwankung. Allerdings muss der zeitliche Mittelwert der Druckschwankung aus dem Effektivwert von v_max verwendet werden: