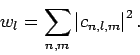Next: Statistik der Messwerten im
Up: Hermite'sche Operatoren. Fall des
Previous: Hermite'sche Operatoren. Fall des
Contents
Nehmen wir an, dass der Operator  ein VONS der Eigenfunktionen
ein VONS der Eigenfunktionen
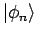 (Eigenwerte
(Eigenwerte 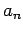 ) besitzt (Beispiele sind
alle unsere Hamilton-Operatoren). Betrachten wir
) besitzt (Beispiele sind
alle unsere Hamilton-Operatoren). Betrachten wir 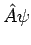 :
:
Diese Reihe konvergiert falls
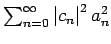 konvergiert.
konvergiert.
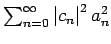 gleicht dann der Norm von
gleicht dann der Norm von
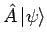 . Das ist also ein Kriterium, dass
. Das ist also ein Kriterium, dass
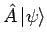 dem
Hilbert-Raum angehört.
dem
Hilbert-Raum angehört.
Diese Eigenschaft erlaubt, die Funktionen von Operatoren  zu
definieren: Der Operator
zu
definieren: Der Operator 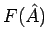 ist definiert durch seine Einwirkung
auf die Fkt.
ist definiert durch seine Einwirkung
auf die Fkt. 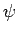 so dass
so dass
Der Operator 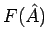 ist eindeutig definiert, falls die Reihe
ist eindeutig definiert, falls die Reihe
konvergiert.
Bemerkungen:
- Die Fkt.
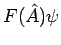 hängt nicht von einer konkreter Wahl
von dem Basis
hängt nicht von einer konkreter Wahl
von dem Basis
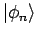 .
.
- Das Gleiche gilt, wenn die Basisfunktionen durch mehreren Zahlen
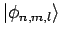 numeriert werden.
numeriert werden.
Betrachten wir nun einen Operator
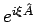 definiert für alle
definiert für alle 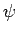 :
:
die Reihe konvergiert für alle
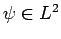 da
da
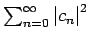 für solche Funktionen konvergiert. Wir nehmen
jetzt
für solche Funktionen konvergiert. Wir nehmen
jetzt 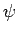 als normiert an, d.h.
als normiert an, d.h.
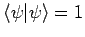 .
.
Jetzt können wir die Verteilung der Werte einer physikalischen Messgröße
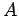 für jeden Zustand
für jeden Zustand 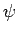 definieren: In der Wahrscheinlichkeitsrechnung
ist
definieren: In der Wahrscheinlichkeitsrechnung
ist
die charakteristische Funktion der Wahrscheinlichkeitsverteilung
mit Dichte 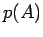 . Im klassischen Fall gilt dann (in 1d)
. Im klassischen Fall gilt dann (in 1d)
(Bemerkung: Korrektere Betrachtung benutzt die Notation eines
Stiltjes-Integrals: Wenn 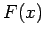 die Wahrscheinlichkeit davon ist, dass
die Wahrscheinlichkeit davon ist, dass 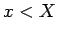 ,
so
,
so
Falls die Dichte 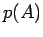 existiert, so ist
existiert, so ist 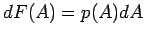 .)
.)
Die Verteilungsdichte 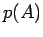 folgt durch inverse Fourier-Transform
folgt durch inverse Fourier-Transform
Wir postulieren nun, dass auch in Quantenmechanik
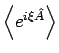 die charakteristische Funktion die
entsprechende Verteilung der Messwerte von
die charakteristische Funktion die
entsprechende Verteilung der Messwerte von 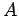 darstellt. Es gilt
darstellt. Es gilt
mit
Die Rücktransformation von 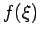 ergibt dann
ergibt dann
Der Wert von 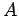 kann nur die Werte von
kann nur die Werte von 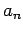 annehmen, d.h. nur der
Eigenwerten des entsprechenden Operators
annehmen, d.h. nur der
Eigenwerten des entsprechenden Operators  . Aus der
Parceval-Identität folgt dass
. Aus der
Parceval-Identität folgt dass
d.h. die Wahrscheinlichkeiten sind richtig normiert.
I.A. ist ein Mittelwert von einer Funktion 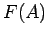
Damit 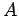 einen scharfen, festen Wert annimmt, ist es notwendig und hinreichend,
dass
einen scharfen, festen Wert annimmt, ist es notwendig und hinreichend,
dass 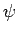 eine Eigenfunktion von
eine Eigenfunktion von  ist.
ist.
Bemerkung: Charakterisiert man eine WF durch mehreren Indices, z.B.
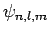 , (wie für das Wasserstoffatom) wovon
, (wie für das Wasserstoffatom) wovon 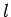 die Eigenfkt.
von
die Eigenfkt.
von 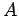 (sagen wir
(sagen wir 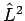 ) numerieren, so ist
) numerieren, so ist
Man kann auch unabhängig von der charakteristischen Funktion postulieren,
dass
- Die möglichen Messergebnisse
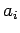 entsprechen
den Eigenwerten des Operators
entsprechen
den Eigenwerten des Operators  . Die
Messwahrscheinlichkeiten entsprechen
. Die
Messwahrscheinlichkeiten entsprechen
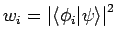 .
.




Next: Statistik der Messwerten im
Up: Hermite'sche Operatoren. Fall des
Previous: Hermite'sche Operatoren. Fall des
Contents
Prof. Igor Sokolov
2005-02-14
![]() ein VONS der Eigenfunktionen
ein VONS der Eigenfunktionen
![]() (Eigenwerte
(Eigenwerte ![]() ) besitzt (Beispiele sind
alle unsere Hamilton-Operatoren). Betrachten wir
) besitzt (Beispiele sind
alle unsere Hamilton-Operatoren). Betrachten wir ![]() :
:
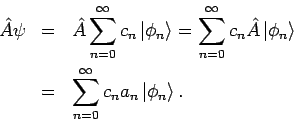
![]() zu
definieren: Der Operator
zu
definieren: Der Operator ![]() ist definiert durch seine Einwirkung
auf die Fkt.
ist definiert durch seine Einwirkung
auf die Fkt. ![]() so dass
so dass
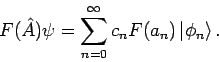
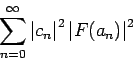
![]() definiert für alle
definiert für alle ![]() :
:
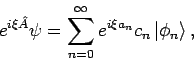
![]() für jeden Zustand
für jeden Zustand ![]() definieren: In der Wahrscheinlichkeitsrechnung
ist
definieren: In der Wahrscheinlichkeitsrechnung
ist
![]() folgt durch inverse Fourier-Transform
folgt durch inverse Fourier-Transform
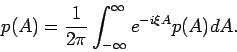
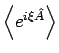 die charakteristische Funktion die
entsprechende Verteilung der Messwerte von
die charakteristische Funktion die
entsprechende Verteilung der Messwerte von 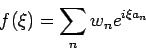
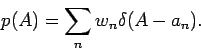
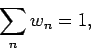
![]()
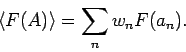
![]() , (wie für das Wasserstoffatom) wovon
, (wie für das Wasserstoffatom) wovon ![]() die Eigenfkt.
von
die Eigenfkt.
von ![]() (sagen wir
(sagen wir ![]() ) numerieren, so ist
) numerieren, so ist