Nächste Seite: Exakte Statistik nichtwechselwirkender Teilchen
Aufwärts: Die Großkanonische Zustandssumme
Vorherige Seite: Die Großkanonische Zustandssumme
Bestimmung der mittleren quadratischen Schwankung der Teilchenzahl.
Der Mittelwert einer beliebigen physikalischen Größe 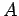 ist
ist
(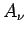 ist der Wert von
ist der Wert von 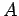 im Zustand
im Zustand 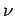 des Systems). Somit gilt
des Systems). Somit gilt
und
Dann ist die mittlere quadratische Schwankung
Nun ist
Dann

Aus Gl.(6) folgt für ein Idealgas, dass
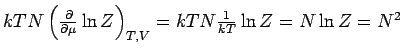 (die letzte Gleichung folgt aus Gl.(8)). Außerdem
gilt:
(die letzte Gleichung folgt aus Gl.(8)). Außerdem
gilt:
Unter Benutzung der Gl.(10) und der Zustandsgleichung 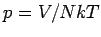 bekommt man
bekommt man
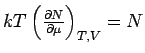 .
. 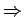
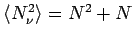 . Schließlich, ergibt sich
. Schließlich, ergibt sich
Die mittlere relative Schwankung ist damit
Für die Ableitung ist eine statistische Betrachtung nötig: das
Ergebnis liegt außerhalb der Reichweite der Thermodynamik.



Nächste Seite: Exakte Statistik nichtwechselwirkender Teilchen
Aufwärts: Die Großkanonische Zustandssumme
Vorherige Seite: Die Großkanonische Zustandssumme
Prof. Igor Sokolov
2004-07-01
![]() ist
ist
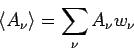
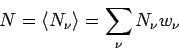
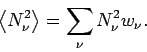
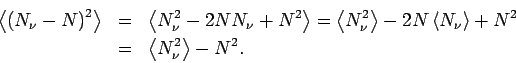
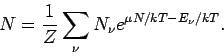
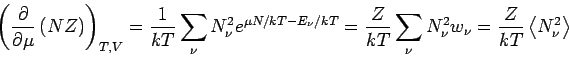
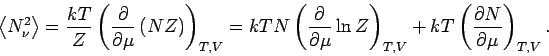
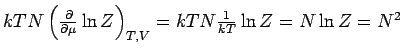 (die letzte Gleichung folgt aus Gl.(8)). Außerdem
gilt:
(die letzte Gleichung folgt aus Gl.(8)). Außerdem
gilt:
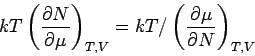
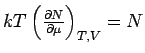 .
.